Mathe ↠ Lineare Gleichungssysteme ↠ Grafisches Lösungsverfahren

Grafisches Lösungsverfahren

Beim grafischen Lösungsverfahren stellt man sich die linearen Gleichungen als lineare Funktion vor.

!

Merke

Ein Lineares Gleichungssystem kann unterschiedliche Lösungen haben, welche man grafisch folgendermaßen herausfinden kann:
  • eine Lösung: die Geraden schneiden sich in einem Punkt
  • keine Lösung: die Geraden sind parallel zueinander
  • unendlich viele Lösung: die Geraden sind identisch
i

Vorgehensweise

  1. Die Gleichungen passend umstellen.
  2. Die Graphen der Gleichungen in ein Koordinatensystem einzeichnen.
  3. Schnittpunkt ablesen.

Beispiel

Bestimme grafisch die Lösungsmenge des Linearen Gleichungssystems:

  1. $4x=4y-8$
  2. $y-6=-x$

  1. Die Gleichungen passend umstellen

    $4x=4y-8$   $|:4$
    $x=y-2$   $|+2$
    $\color{green}{y=x+2}$

    $y-6=-x$   $|+6$
    $\color{blue}{y=-x+6}$

  2. Die Geraden in ein Koordinatensystem einzeichnen

    $\color{green}{f(x)=x+2}$
    $\color{blue}{g(x)=-x+6}$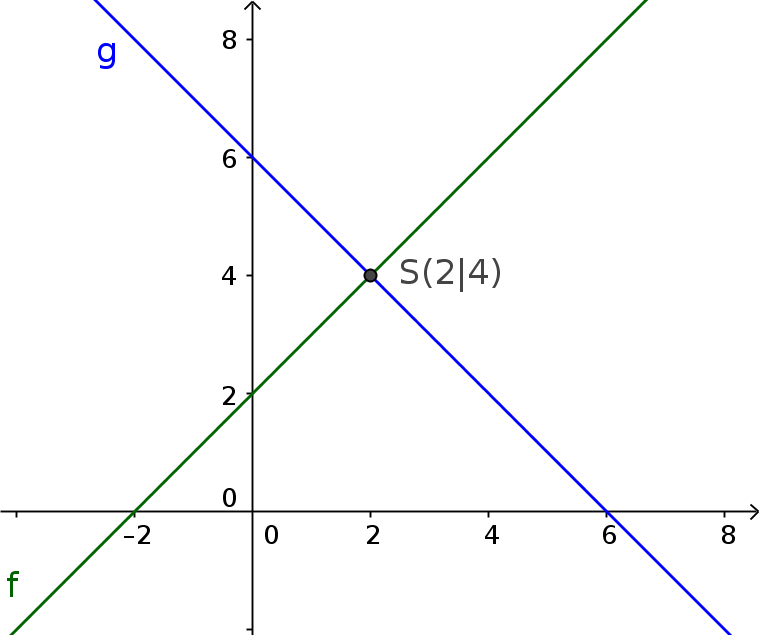

    Grafisches Lösungsverfahren

  3. Schnittpunkt bestimmen und Lösungsmenge angeben

    Ein Schnittpunkt: $S(2|4)$
    => Es gibt eine Lösung

    $L=\{(2|4)\}$

Graphisch lösen: Lineare Gleichungssysteme (LGS) lösen

Kooperation mit dem Kanal von Mister Mathe

Mit dem Abspielen dieses Videos akzeptierst du YouTubes Datenschutzerklärung.

Videos von YouTube immer laden

Um ein lineares Gleichungssystem graphisch zu lösen, muss dieses sinnvoll im Koordinatensystem dargestellt werden können. Dazu wird jede Gleichung so umgestellt, dass wir die Funktionsgleichung einer linearen Funktion erhalten.

Bei zwei linearen Gleichungen der Form $ax+by=c$ mit den zwei Unbekannten $x$ und $y$ werden diese nach $y$ umgestellt.

$y=mx+n$

Graphen zeichnen

Die beiden linearen Funktionen können nun in das gleiche Koordinatensystem eingezeichnet werden. Für die Funktionen werden dazu jeweils zwei Punkte bestimmt:

  1. Punkt $P(0|n)$ mit y-Achsenabschnitt $n$ bestimmen
  2. Zweiten Punkt mit der Steigung $m$ berechnen
  3. Gerade durch beide Punkte ziehen

Wenn beide Geraden einen gemeinsamen Schnittpunkt haben, dann ist dieser die Lösung des LGS. Das lineare Gleichungssystem hat dann genau eine Lösung.

keine Lösung: Lineare Gleichungssysteme (LGS) lösen

Kooperation mit dem Kanal von Mister Mathe

Mit dem Abspielen dieses Videos akzeptierst du YouTubes Datenschutzerklärung.

Videos von YouTube immer laden

Wenn die beiden eingezeichneten Geraden echt parallel sind, gibt es keinen Schnittpunkt. Das lineare Gleichungssystem hat dann keine Lösung.

i

Tipp

In umgestellter Form lässt sich dieses Szenario einfach erkennen: Beide Geradengleichungen haben die gleiche Steigung $m$ aber unterschiedliche y-Achsenabschnitte $n$.

Beispiel

  1. $y=2x+\color{red}{3}$
  2. $y=2x+\color{red}{6}$

Die Steigungen $m_1=m_2=2$ sind gleich, aber $n_1=3\neq6=n_2$. Die Geraden verlaufen parallel ohne gemeinsame Punkte. Das Gleichungssystem ist unlösbar.

Unendlich viele Lösungen: Lineare Gleichungssysteme (LGS) lösen

Kooperation mit dem Kanal von Mister Mathe

Mit dem Abspielen dieses Videos akzeptierst du YouTubes Datenschutzerklärung.

Videos von YouTube immer laden

Wenn die beiden eingezeichneten Geraden identisch sind, gibt es keinen Schnittpunkt. Das lineare Gleichungssystem hat dann unendlich viele Lösungen.

i

Info

In umgestellter Form ist dies direkt zu erkennen, denn es handelt sich um die gleichen Funktionsgleichungen. Sowohl die Steigung $m$ als auch der y-Achsenabschnitt $n$ sind identisch.

Beispiel

  1. $y=2x+3$
  2. $y=2x+3$

Die Steigungen $m_1=m_2=2$ und Achsenabschnitte $n_1=n_2=3$ sind gleich. Es handelt sich beim Graphen also um identische Geraden. Es gibt unendlich viele Lösungen für das LGS.