Math ↠ Systems of linear equations ↠ Graphical method

Graphical method

In the graphical method one imagines the linear equations as a linear function.

!

Remember

A system of linear equations can have different solutions, which can be found graphically as follows:
  • one solution: the straight lines intersect at one point
  • no solution: the straight lines are parallel to each other
  • infinitely many solution: the straight lines are identical
i

Method

  1. Convert the equations appropriately.
  2. Draw the graphs of the equations into a coordinate system.
  3. Read off intersection.

Example

Determine graphically the solution set of the system of linear equations:

  1. $4x=4y-8$
  2. $y-6=-x$

  1. Convert the equations appropriately

    $4x=4y-8$   $|:4$
    $x=y-2$   $|+2$
    $\color{green}{y=x+2}$

    $y-6=-x$   $|:+6$
    $\color{blue}{y=-x+6}$

  2. Draw the lines in a coordinate system

    $\color{green}{f(x)=x+2}$
    $\color{blue}{g(x)=-x+6}$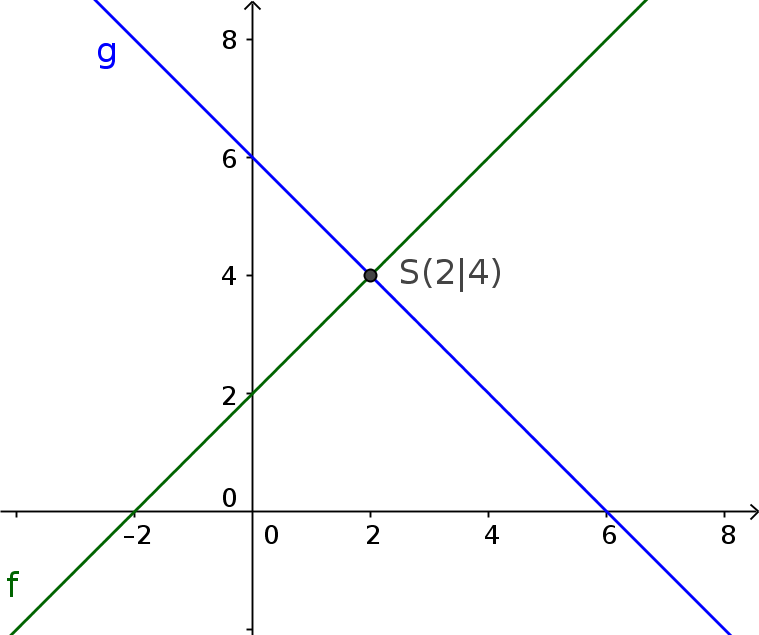

  3. Determine the intersection and specify the solution set

    One intersection: $I(2|4)$
    => There is one solution

    $S=\{(2|4)\}$