Lineare Gleichungssysteme

Als lineares Gleichungssystem werden mehrere zusammenhängende lineare Gleichungen mit mindestens zwei Variablen bezeichnet. Wir beschäftigen uns in diesem Artikel damit, was man unter einem linearen Gleichungssystem oder LGS versteht, welche Lösungsverfahren es gibt und wie sich lineare Gleichungen eines Gleichungssystems grafisch darstellen lassen.

Lineare Gleichungen

Lineare Gleichungen sind Gleichungen ersten Grades. Sie besitzen daher keine Variablen in höherer Potenz (z. B. $x^2$ oder $x^3$). Die Lösung der Gleichung bei einer Variable ist eindeutig.

Allgemeine Form: $ax+b=0$

Beispiel

$3x+15=0$ mit der Lösung $x=-5$

Lineare Gleichungen mit zwei Variablen

Gleichungen können auch mehrere Unbekannte besitzen, zum Beispiel lineare Gleichungen mit zwei Variablen. Diese haben unendlich viele gültige Lösungen.

Allgemeine Form: $ax+by=c$

Beispiel

$3x+10y=10$ mit der Lösung $x=0; y=1$ oder $x=10;y=-2$ oder $x=5;y=-\frac12$

Lösen linearer Gleichungssysteme

Mehrere lineare Gleichungen mit mehreren Variablen bilden ein lineares Gleichungssystem. Dabei werden zum Lösen des LGS mindestens so viele Gleichungen wie Variablen benötigt. Um ein lineares Gleichungssystem mit zwei Variablen zu lösen, werden auch zwei lineare Gleichungen benötigt.

Folgende Möglichkeiten gibt es, um ein lineares Gleichungssystem zu lösen:

• Grafisches Lösungsverfahren
• Einsetzungsverfahren
• Gleichsetzungsverfahren
• Additionsverfahren

Graphisches Lösungsverfahren

Ein lineares Gleichungssystem kann entweder eine, keine oder unendlich viele Lösungen haben. Bei der graphischen Lösung mit Hilfe von linearen Funktionen sind die Lösungen folgendermaßen zu unterscheiden:

• eine Lösung: die Geraden schneiden sich in einem Punkt
• keine Lösung: die Geraden sind parallel zueinander
• unendlich viele Lösung: die Geraden sind identisch

Beispiel

1. $4x=4y-8$ wird umgestellt zu $\color{green}{f(x)=x+2}$
2. $y-6=-x$ wird umgestellt zu $\color{blue}{g(x)=-x+6}$

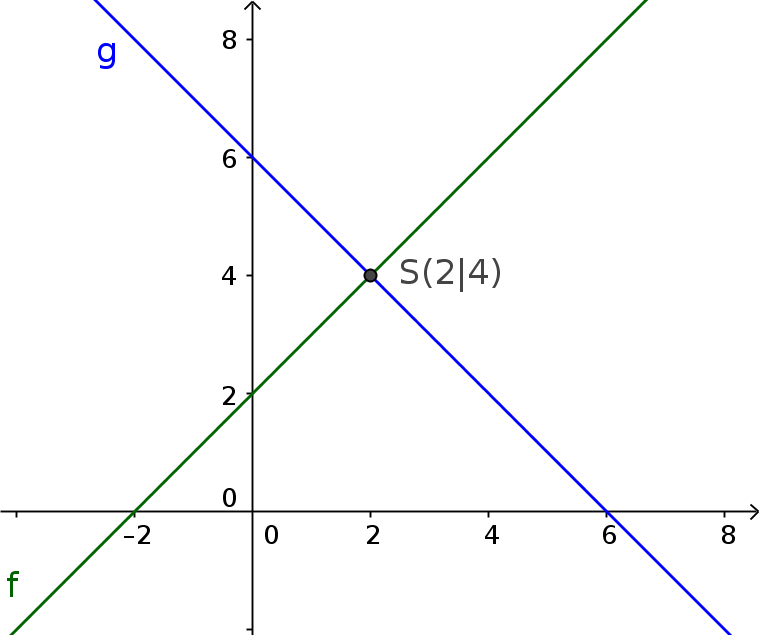
Der Schnittpunkt $S(2|4)$ ist die Lösung des Gleichungssystems