Bestimmen vom y-Achsenabschnitt n
Der y-Achsenabschnitt (Ordinatenabschnitt) $n$ kann man mithilfe der Steigung $m$ und einem Punkt $P_{ 1 }(x_{ 1 }|y_{ 1 })$ berechnen, indem man diese in die allgemeine Gleichung einsetzt und umstellt:
$y_{ 1 }=m\cdot x_{ 1 }+n$
$n=y_{ 1 }-m\cdot x_{ 1 }$
$n=y_{ 1 }-m\cdot x_{ 1 }$
i
Tipp
Meistens ist es möglich den y-Achsenabschnitt von der Geraden am Punkt $P(0|n)$ abzulesen. Dafür an der Stelle $x = 0$ den $y$-Wert ablesen.
Beispiel
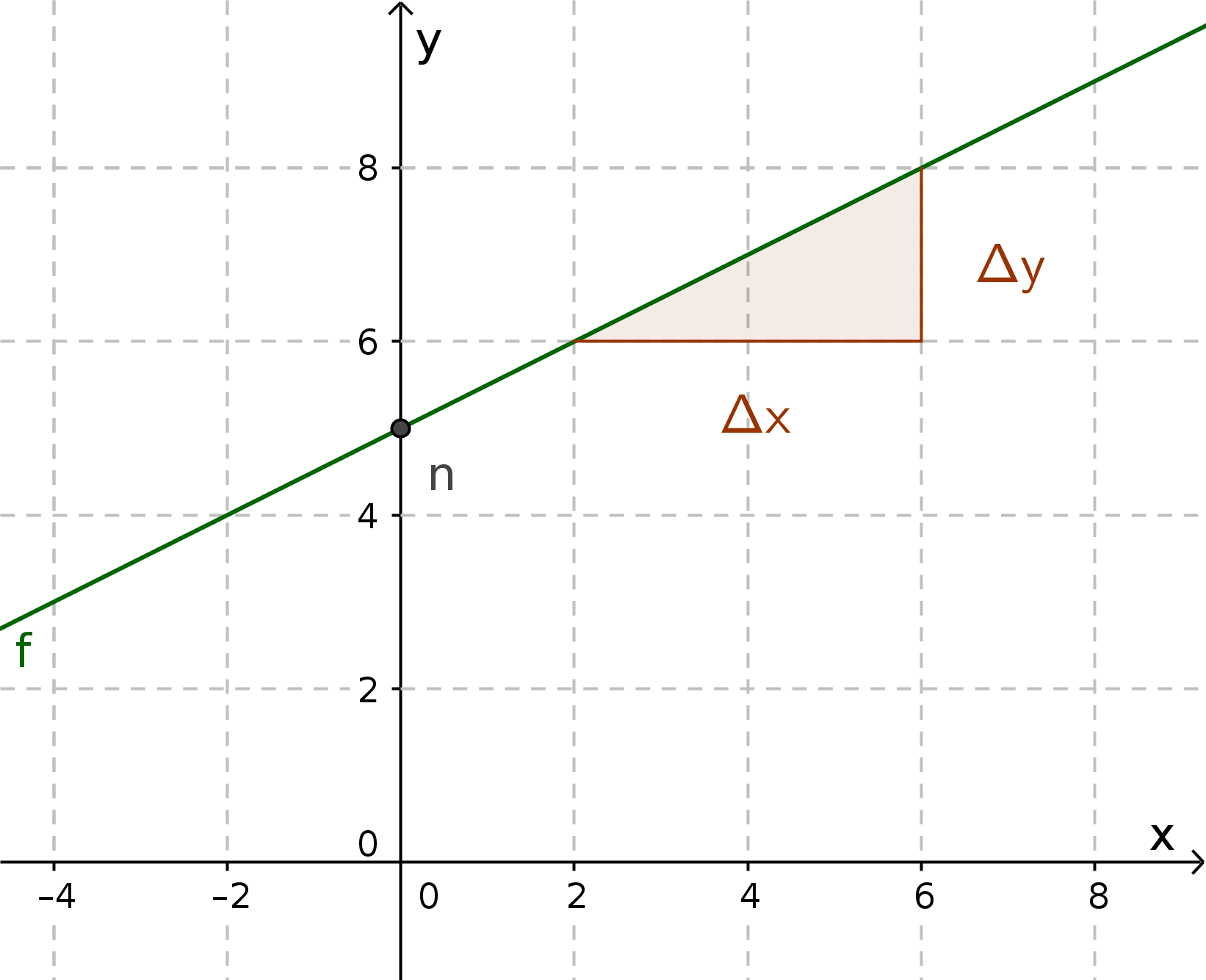
2 Punkte ablesen z.B.
$P_{ 1 }(2|6)$ und $P_{ 2 }(6|8)$Steigung berechnen
$m=\frac{ \Delta y }{ \Delta x }=\frac{ y_{ 2 } - y_{ 1 } }{ x_{ 2 }-x_{ 1 } }=\frac{ 8-6 }{ 6-2 }=\frac{ 2 }{ 4 }=0,5$Steigung $m=0,5$ und $P_{ 1 }(2|6)$ in die Gleichung einsetzen
$n=y_{ 1 }-m\cdot x_{ 1 }=6-0,5\cdot 2=5$y-Achsenabschnitt $n=5$ und Steigung $m=0,5$ in $y=mx+n$ einsetzen
$y=0,5x+5$
y-Achsenabschnitt Gerade berechnen, Punkt & Steigung, Schnittpunkt mit der y-Achse, lineare Funktion
Kooperation mit dem Kanal von Mister Mathe

