Bestimmen der Steigung m
Um die Steigung $m$ zu berechnen, benötigt man 2 beliebige Punkte auf der Geraden: $P_{ 1 }(x_{ 1 }|y_{ 1 })$ und $P_{ 2 }(x_{ 2 }|y_{ 2 })$.
Man kann die Steigung mit einem Steigungsdreieck bestimmen, indem man sich 2 Punkte auf der Geraden auswählt und den Abstand in x- und in y-Richtung ermittelt.
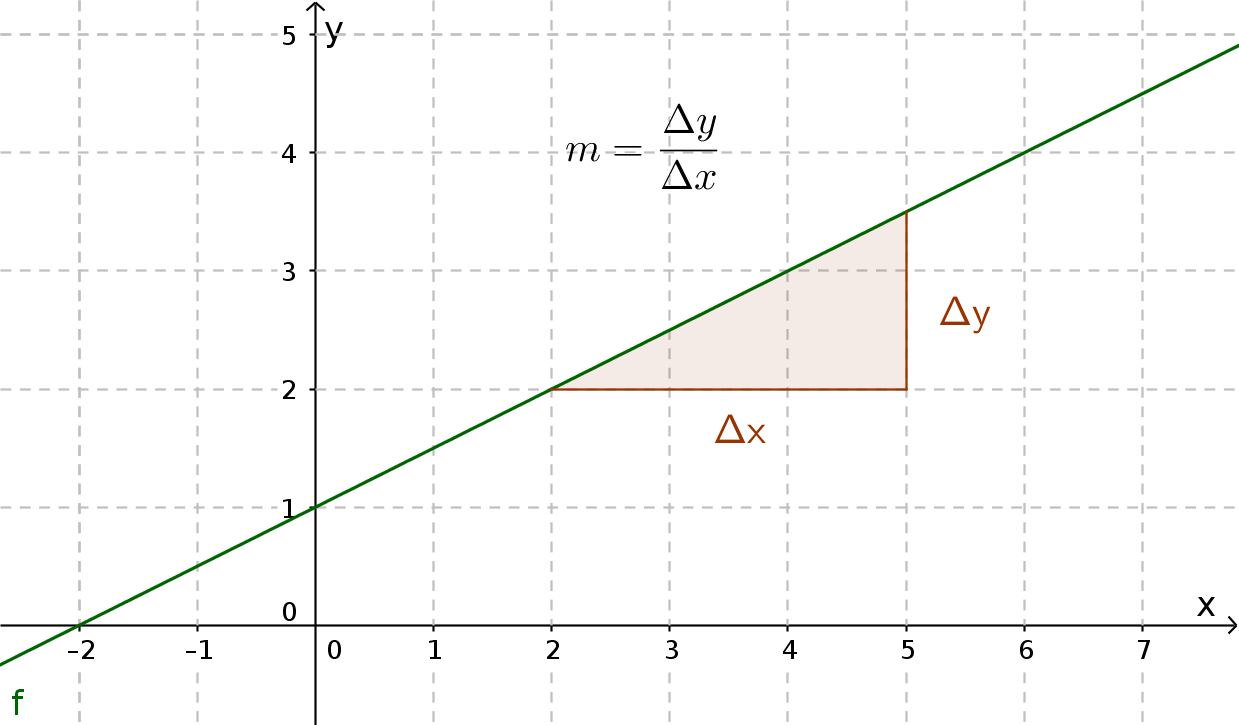
Alternativ kann man die $x$- und $y$-Werte der Punkte auch in folgende Formel einsetzen:
$m=\frac{ \Delta y }{ \Delta x }=\frac{ y_{ 2 } - y_{ 1 } }{ x_{ 2 }-x_{ 1 } }$
Beispiel
Bestimme die Steigung der Geraden.
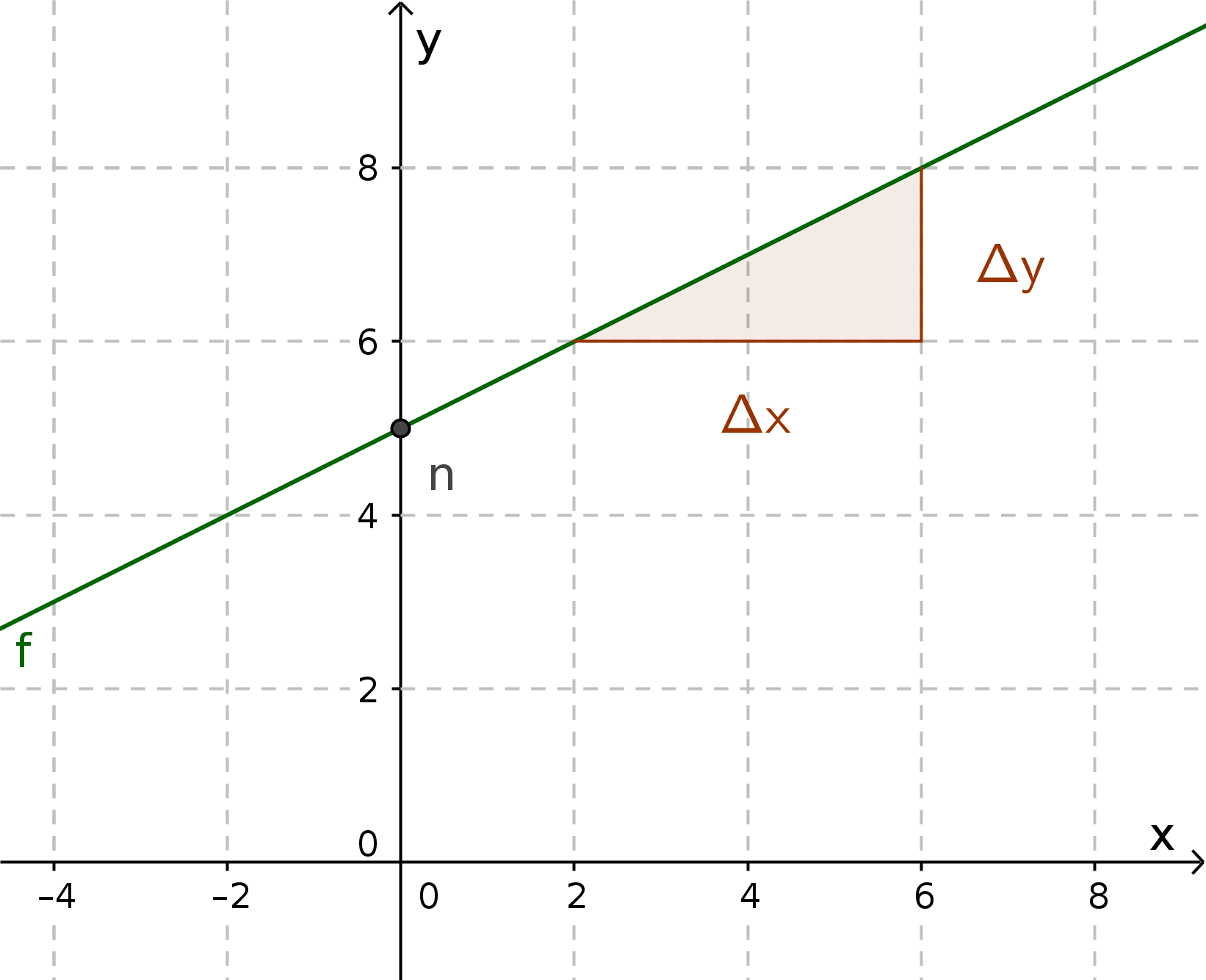
2 Punkte ablesen, z.B.:
$P_{ 1 }(2|6)$ und $P_{ 2 }(6|8)$Punkte in Formel einsetzen und ausrechnen:
$m=\frac{ \Delta y }{ \Delta x }=\frac{ y_{ 2 } - y_{ 1 } }{ x_{ 2 }-x_{ 1 } }=\frac{ 8-6 }{ 6-2 }=\frac{ 2 }{ 4 }=0,5$Steigung $m=0,5$ in $y=mx+n$ einsetzen:
$y=0,5x+n$
Steigung Gerade berechnen, Beispiel, Steigungsdreieck, Steigung aus zwei Punkten, lineare Funktion
Kooperation mit dem Kanal von Mister Mathe
!
Merke
Die Steigung einer linearen Funktion gibt an, wie steil sie nach oben oder unten verläuft.
Die Steigung $m$ kann positiv oder negativ sein.
- $m>0$: Gerade verläuft nach oben (steigend)
- $m<0$: Gerade verläuft nach unten (fallend)