Determine the slope m

To calculate the slope $m$, you need 2 arbitrary points on the line: $P_{ 1 }(x_{ 1 }|y_{ 1 })$ and $P_{ 2 }(x_{ 2 }|y_{ 2 })$.
You can determine the slope with a gradient triangle by selecting 2 points on the line and determining the distance in the x and y directions.

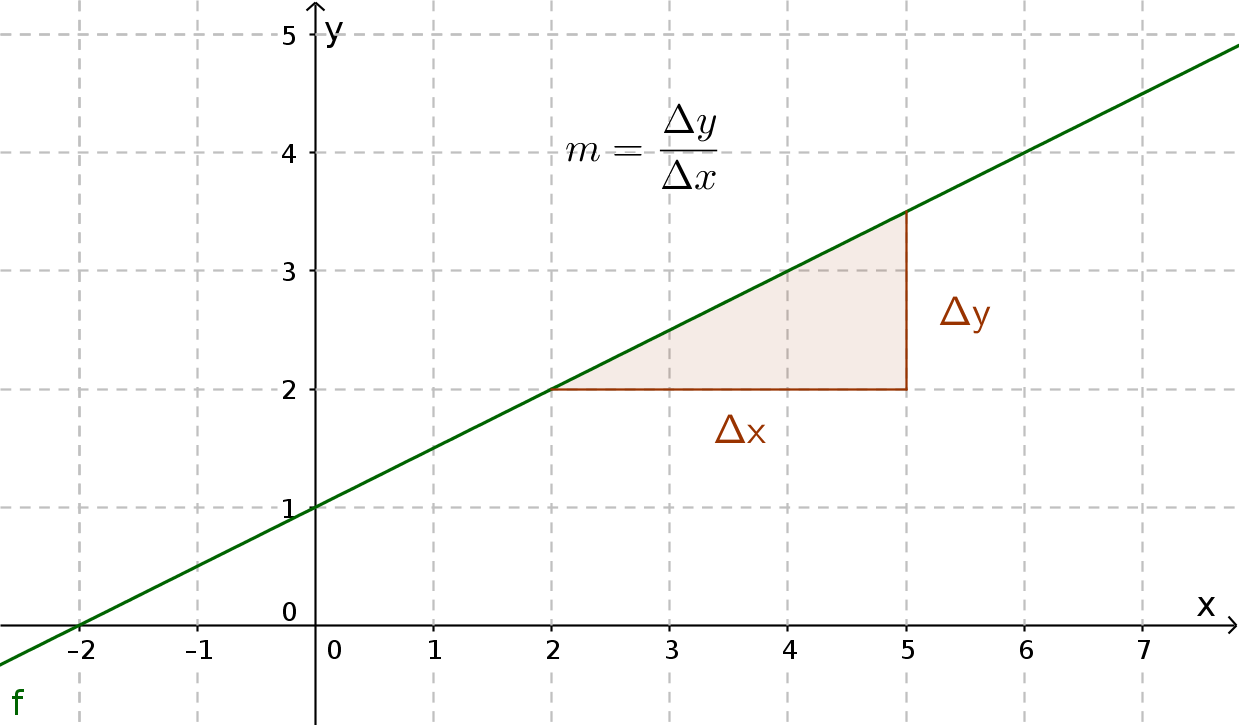
Alternatively, the $x$ and $y$ values of the points can also be used in the following formula:

Example

Determine the slope of the line.

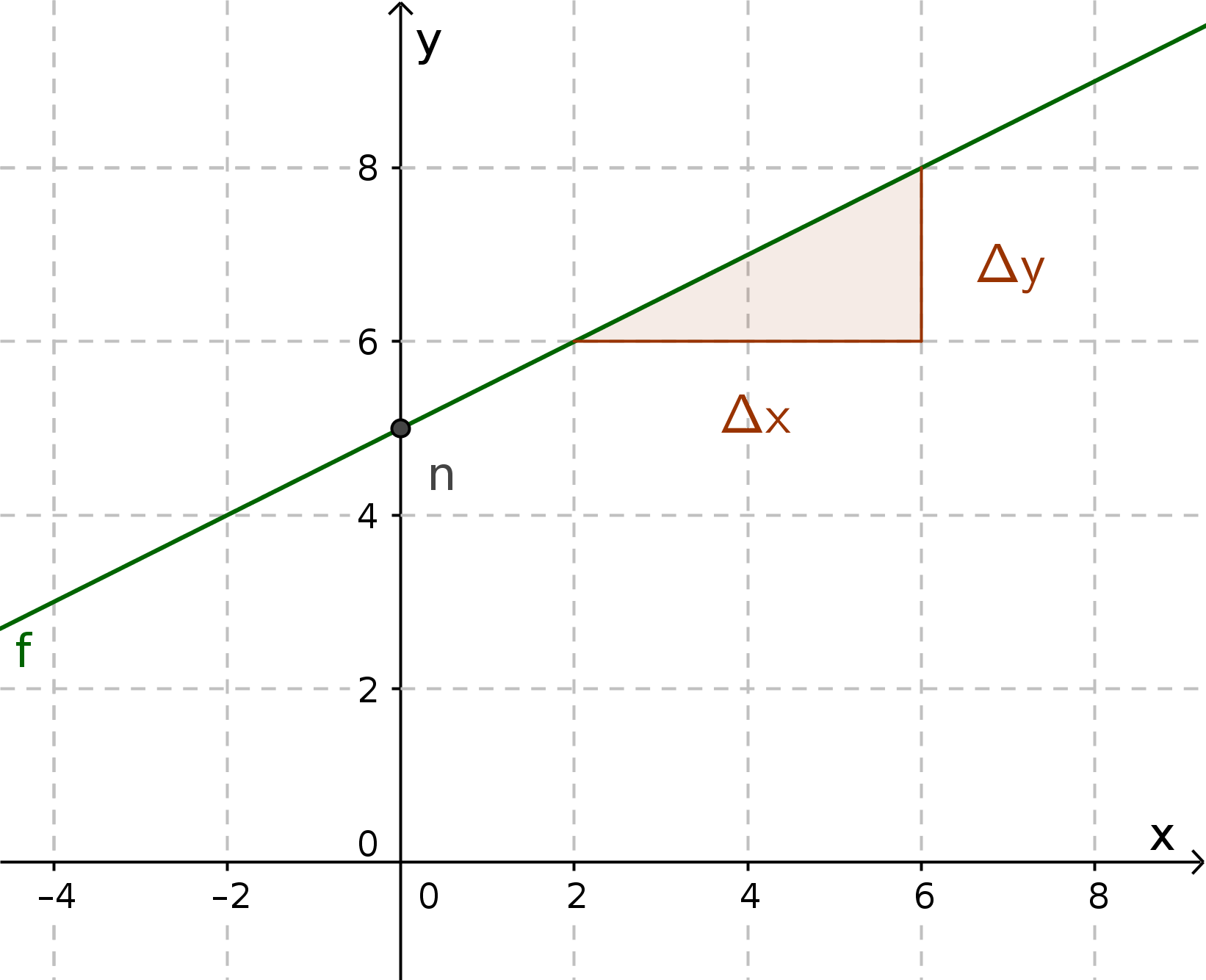
1. Read 2 points, e.g.:

   
   $P_{ 1 }(2|6)$ und $P_{ 2 }(6|8)$

2. Insert points in formula and calculate:

   
   $m=\frac{ \Delta y }{ \Delta x }=\frac{ y_{ 2 } - y_{ 1 } }{ x_{ 2 }-x_{ 1 } }=\frac{ 8-6 }{ 6-2 }=\frac{ 2 }{ 4 }=0.5$

3. Use slope $m=0.5$ in $y=mx+n$:

   
   $y=0.5x+n$