Определите наклон прямой m

Для определения наклона $m$, вам нужны 2 произвольных точки на прямой: $P_{ 1 }(x_{ 1 }|y_{ 1 })$ и $P_{ 2 }(x_{ 2 }|y_{ 2 })$.
Вы можете определить наклон с помощью градиентного треугольника, выбрав 2 точки на прямой и определив расстояние в направлении х и y .

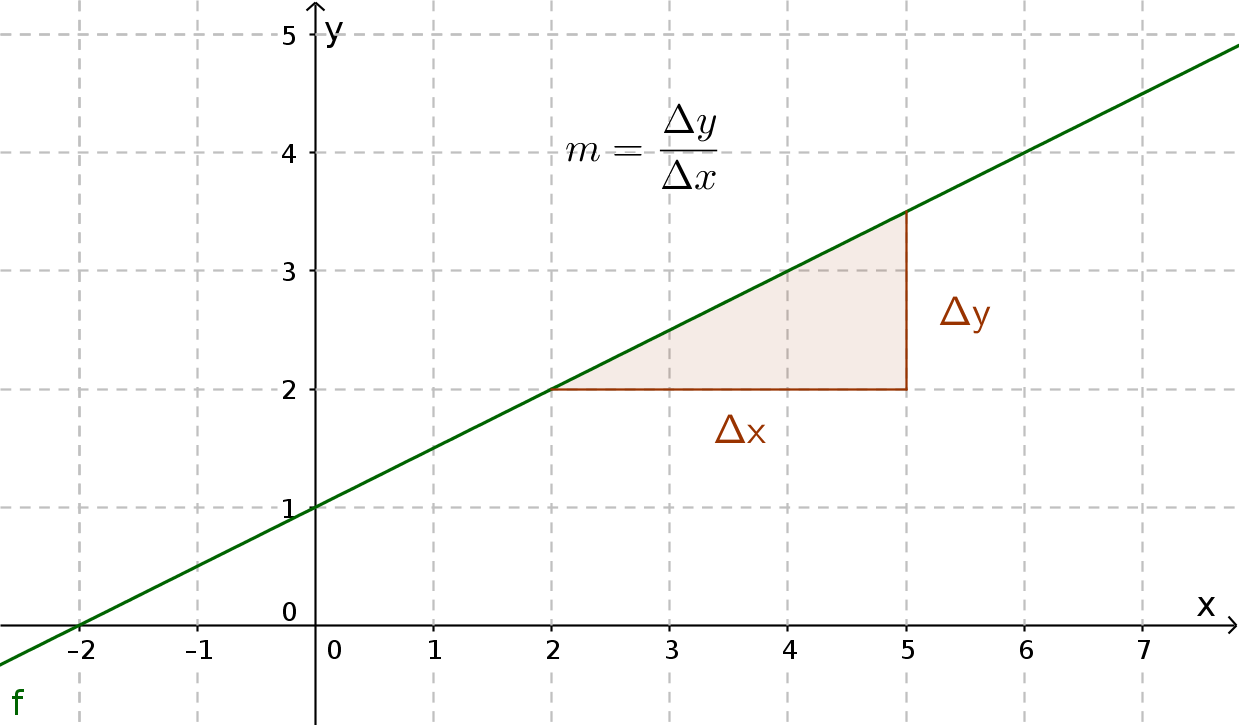
В качестве альтернативы, $x$ и $y$ значения координат также могут быть использованы в следующей формуле:

Например

Определите наклон прямой.

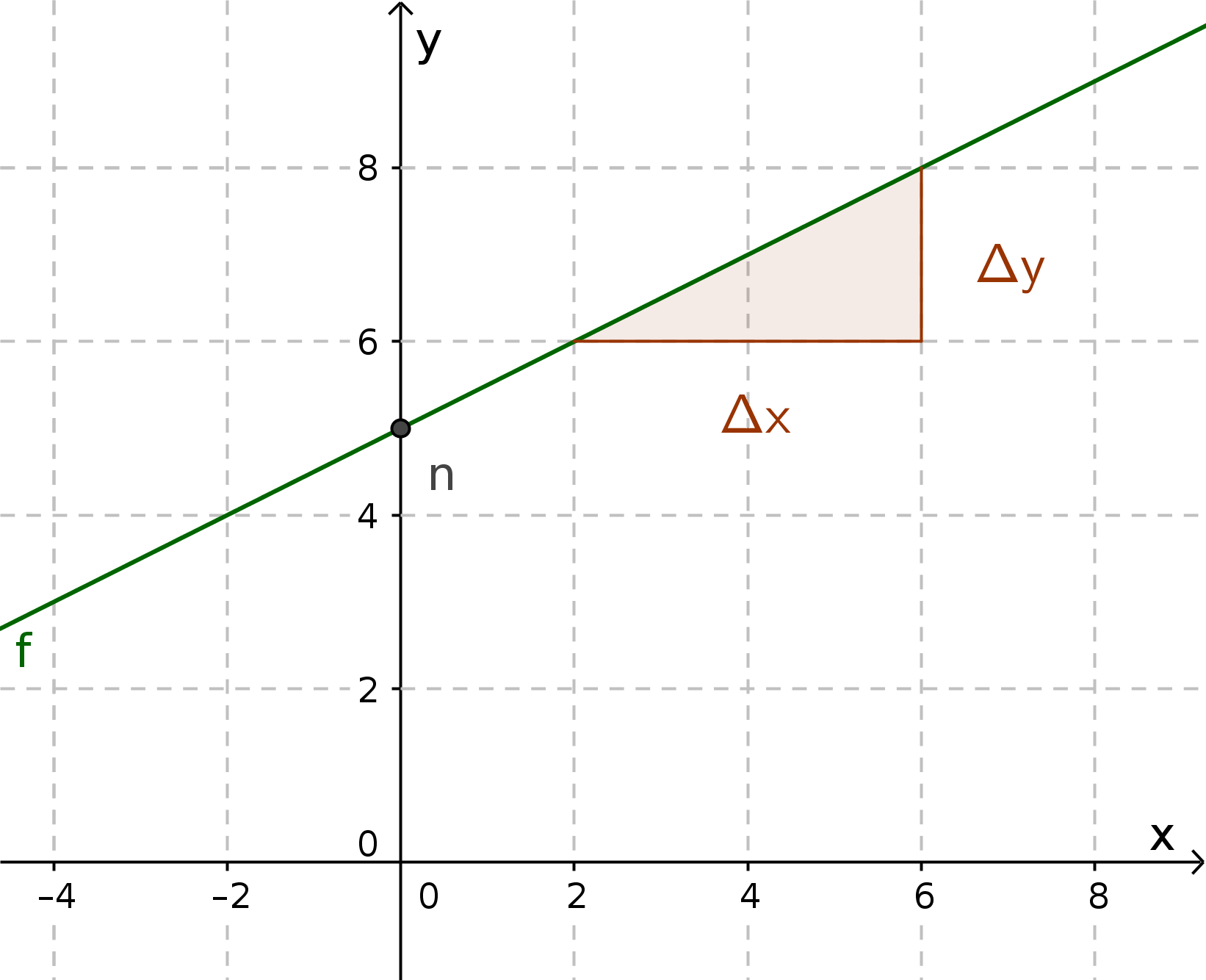
1. Возьмите 2 точки, нап.:

   
   $P_{ 1 }(2|6)$ и $P_{ 2 }(6|8)$

2. Подставьте точки в формулу и вычислите:

   
   $m=\frac{ \Delta y }{ \Delta x }=\frac{ y_{ 2 } - y_{ 1 } }{ x_{ 2 }-x_{ 1 } }=\frac{ 8-6 }{ 6-2 }=\frac{ 2 }{ 4 }=0.5$

3. Используйте наклон $m=0.5$ в $y=mx+n$:

   
   $y=0.5x+n$