Mathe ↠ Kurvendiskussion ↠ Extrempunkte

Extrempunkte

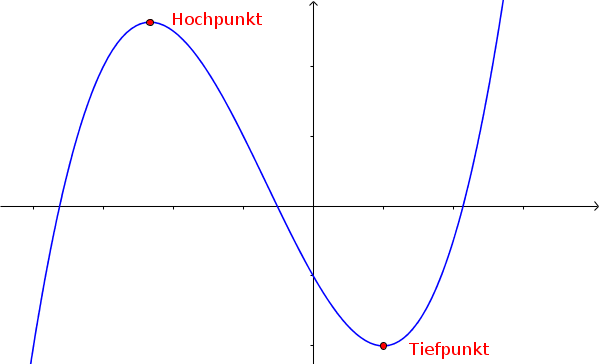
Die Hoch- und Tiefpunkte eines Funktionsgraphen bezeichnet man als Extrempunkte.

!

Merke

Notwendiges Kriterium

Voraussetzung für das Vorhandensein von Extrempunkten ist, dass die erste Ableitung an dieser Stelle eine Nullstelle besitzt:
$f'(x_E)=0$

Hinreichendes Kriterium

Ob es sich nun um einen Hoch-, Tiefpunkt oder keines von beidem handelt, ist abhängig von der zweiten Ableitung
Es liegt ein

  • Hochpunkt vor, wenn gilt $f''(x_E)<0$
  • Tiefpunkt vor, wenn gilt $f''(x_E)>0$
Hochpunkt und Tiefpunkt
i

Vorgehensweise

  1. Ableitungen bestimmen
  2. Nullstelle(n) der ersten Ableitung berechnen
  3. Nullstelle(n) in die zweite Ableitung einsetzen
  4. Extrempunkt(e) angeben

Beispiel

Bestimme die Extrempunkte der Funktion $f(x)=x^3+2x^2-4x-8$.

  1. Ableitungen bestimmen

    $f'(x)=3x^2+4x-4$
    $f''(x)=6x+4$

  2. Nullstellen der Ableitung berechnen

    Es liegt eine quadratische Gleichung vor, die man beispielsweise mit der PQ-Formel lösen kann.
    $f'(x)=3x^2+4x-4$
    $x_E\Leftrightarrow f'(x_E)=0$

    $3x^2+4x-4=0\quad|:3$
    $x^2+\frac43x-\frac43=0$
    $x_{1,2} = -\frac{p}{2} \pm\sqrt{(\frac{p}{2})^2-q}$
    $x_{1,2} = -\frac{2}{3} \pm\sqrt{(\frac23)^2+\frac43}$
    $x_{1,2} = -\frac{2}{3} \pm\sqrt{\frac{16}{9}}$
    $x_{1,2} = -\frac{2}{3} \pm\frac43$
    $x_{E_{1}}=\color{blue}{-2} \quad x_{E_{2}}=\color{green}{\frac23}$

  3. Nullstellen in die zweite Ableitung einsetzen

    Die soeben ermittelten extremwertverdächtigen Stellen setzen wir in die zweite Ableitung ein.
    $f''(x)=6x+4$

    $f''(\color{blue}{-2})=6\cdot\color{blue}{-2}+4=-8<0$
    => an der Stelle $x=-2$ liegt ein Hochpunkt vor
    $f''(\color{green}{\frac23})=6\cdot\color{green}{\frac23}+4=8>0$
    => an der Stelle $x=\frac23$ liegt ein Tiefpunkt vor

    Hinweis: Die berechneten Werte $8$ und $-8$ waren nur zur Überprüfung, ob es sich um einen Hoch- oder Tiefpunkt handelt. Sie werden nicht mehr gebraucht.

  4. Extrempunkte angeben

    Es sollen Hoch- und TiefPUNKTE angegeben werden: Deshalb noch die y-Koordinate mit der ursprünglichen Funktion berechnen.

    $f(\color{blue}{-2})$ $=(\color{blue}{-2})^3+2\cdot(\color{blue}{-2})^2-4\cdot(\color{blue}{-2})-8$ $=0$
    => Hochpunkt: $H(\color{blue}{-2}|0)$

    $f(\color{green}{\frac23})$ $=(\color{green}{\frac23})^3+2\cdot(\color{green}{\frac23})^2-4\cdot\color{green}{\frac23}-8$ $ \approx-9,48$
    => Tiefpunkt: $T(\color{green}{\frac23}|-9,48)$

Extrempunkte bestimmen, Hochpunkt, Tiefpunkt, Kurvendiskussion

Kooperation mit dem Kanal von Mister Mathe

Mit dem Abspielen dieses Videos akzeptierst du YouTubes Datenschutzerklärung.

Videos von YouTube immer laden

Als Voraussetzung, also notwendiges Kriterium, für das Vorhandensein eines Extrempunktes an der Stelle $x_E$ muss die erste Ableitung eine Nullstelle dort besitzen.

$f'(x_E)=0$

Zwar muss das Kriterium erfüllt sein, jedoch reicht dieses alleine nicht aus, um beurteilen zu können, ob nun wirklich ein Extrempunkt vorliegt und wenn ja, welche Art. Daher das hinreichende Kriterium, welches noch die zweite Ableitung einbezieht:

  • Hochpunkt, wenn gilt $f''(x_E)<0$
  • Tiefpunkt, wenn gilt $f''(x_E)>0$

Sollte für $f''(x_E)=0$ gelten, kann dort ein Sattelpunkt (wenn $f'''(x_E)\neq0$) oder ein Extrempunkt vorliegen. Ein Sattelpunkt ist eine besondere Art Wendepunkt.