Krümmungsverhalten
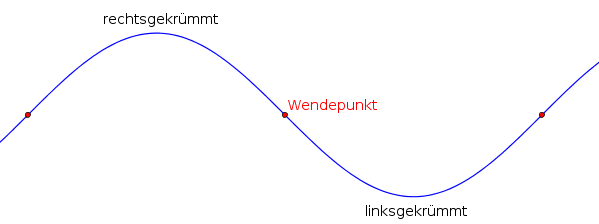
Als Krümmung bezeichnet man die Richtungsänderung eines Funktionsgraphen an einem Punkt (Wendepunkt).
i
Tipp
Als Merkhilfe kann man sich fragen, in welche Richtung man lenken müsste, wenn man den Funktionsgraphen von links nach rechts abfährt.
Die Richtung entscheidet dann ob die Funktion links- oder rechtsgekrümmt ist.
Die Richtung entscheidet dann ob die Funktion links- oder rechtsgekrümmt ist.
!
Merke
Das Krümmungsverhalten in einem Intervall lässt sich mit der zweiten Ableitung bestimmen.
Die Funktion ist auf dem Intervall $I$ zweimal differenzierbar und
Die Funktion ist auf dem Intervall $I$ zweimal differenzierbar und
- linksgekrümmt, wenn für alle $x\in I$ gilt $f''(x)>0$
- rechtsgekrümmt, wenn für alle $x\in I$ gilt $f''(x)<0$
Krümmungsverhalten, Kurvendiskussion, Ableitung, Krümmung, Rechtskrümmung, Linkskrümmung
Kooperation mit dem Kanal von Mister Mathe
Um das Krümmungsverhalten zu bestimmen, sollte man zuerst die Wendestelle berechnen. Danach kann man die Krümmung auf den beiden Seiten des Wendepunktes bestimmen, indem man einen beliebigen Punkt links und einen rechts vom Wendepunkt in die zweite Ableitung einsetzt.

