Wendepunkt

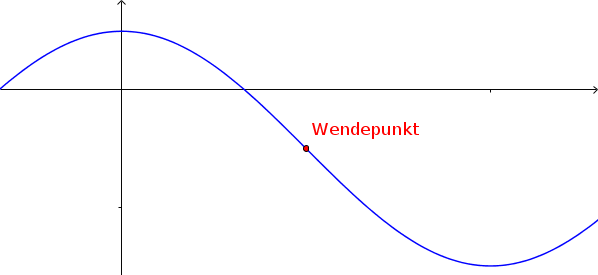
An einem Wendepunkt ändert der Funktionsgraph sein Krümmungsverhalten.

Voraussetzung für das Vorhandensein von Wendepunkten ist, dass die zweite Ableitung an dieser Stelle eine Nullstelle besitzt:
$f''(x_W)=0$

Ein Wendepunkt liegt vor, wenn außerdem gilt:
$f'''(x_W)\neq0$

$Wendepunkt$

Bestimme die Wendepunkte der Funktion $f(x)=x^3+2x^2-4x-8$.

Ableitungen bestimmen
$f'(x)=3x^2+4x-4$ (die erste Ableitung wird nicht gebraucht)
$f''(x)=6x+4$
$f'''(x)=6$
Nullstellen der zweiten Ableitung berechnen
$f''(x)=6x+4$
$x_W\Leftrightarrow f''(x_W)=0$

$6x+4=0\quad|-4$
$6x=-4\quad|:6$
$x_W=-\frac23$
Nullstellen in die dritte Ableitung einsetzen
Die soeben ermittelten Stellen setzen wir in die dritte Ableitung ein.
$f'''(x)=6$

$f'''(-\frac23)=6\neq0$
=> an der Stelle $x=-\frac23$ liegt ein Wendepunkt vor

Hinweis: Der berechnete Wert war ausschließlich zur Überprüfung und wird nicht mehr gebraucht.
Extrempunkte angeben
Es sollen WendePUNKTE angegeben werden: Deshalb noch die y-Koordinate mit der ursprünglichen Funktion berechnen.

$f(-\frac23)$ $=(-\frac23)^3+2\cdot(-\frac23)^2-4\cdot(-\frac23)-8$ $=-4,74$
=> Wendepunkt: $W(-\frac23|-4,74)$

Kooperation mit dem Kanal von Mister Mathe