Kurvendiskussion

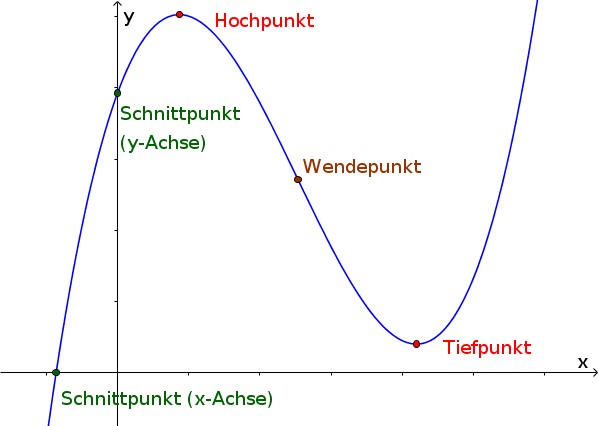
Bei der Kurvendiskussion (Kurvenuntersuchung) untersucht man den Funktionsgraphen auf seine geometrischen Eigenschaften. Dies können besondere Punkte, z. B. Schnittpunkte, Wendepunkte oder Extrempunkte, aber auch das Verhalten wie Montonie, Krümmung oder Symmetrie sein.

Die Kurvendiskussion ist ein Teilgebiet der Differenzialrechnung und steht in starkem Zusammenhang mit der Ableitung, mit deren Hilfe sich viele Eigenschaften ermitteln lassen. Für eine vollständige Kurvenuntersuchung werden zumindest die ersten drei Ableitungen der zu betrachtenden Funktion benötigt. Es bietet sich also an, diese zum Beginn alle aufzustellen.

Achsenschnittpunkte

Ein Funktionsgraph kann mehrere Nullstellen bzw. Schnittpunkte mit der x-Achse haben. Allerdings kann es maximal einen Schnittpunkt mit der y-Achse geben. Es gibt auch Funktionen, deren Graphen gar keine Achsenschnittpunkte haben.

Schnittpunkte mit der y-Achse

Jeder Punkt hat eine x- und eine y-Koordinate. Für einen Schnittpunkt mit der y-Achse ist die x-Koordinate gleich null, sodass man nur die y-Koordinate ausrechnen muss:

Genau wie jede andere y-Koordinate eines Funktionsgraphen erhält man diese durch einfaches einsetzen von $x=0$ in die Funktionsgleichung. Bei linearen Funktionen kann der y-Achsenabschnitt $n$ beispielsweise einfach abgelesen werden.

Schnittpunkte mit der x-Achse

Für den Schnittpunkt mit der x-Achse interessiert einen die entsprechende x-Koordinate, die sogenannte Nullstelle $x_N$. Die y-Koordinate ist 0.

Man erhält die Nullstelle(n), indem die Funktion gleich null gesetzt wird: $x_N\Leftrightarrow f(x_N)=0$

Symmetrieverhalten

Das Symmetrieverhalten gibt Auskunft darüber, ob der Graph einer Funktion zu einer Achse oder einem Punkt symmetrisch ist. Dabei werden zwei Fälle am häufigsten betrachtet:

• Für Achsensymmetrie zur y-Achse muss gelten: $f(-x)=f(x)$
• Für Punktsymmetrie zum Ursprung muss gelten: $f(-x)=-f(x)$

Zur Überprüfung auf das jeweilige Kriterium rechnet man beide Seiten der Gleichung aus und schaut, ob man das gleiche Ergebnis erhält. Wenn ja, ist das Kriterium erfüllt.

Monotonieverhalten

Als Monotonieverhalten bezeichnet man das Steigungsverhalten einer Funktion. Dieses gibt Auskunft darüber, wann eine Funktion steigt oder fällt. Eine Funktion ist für zwei Stellen $x_1$ und $x_2$ mit $x_1 < x_2$

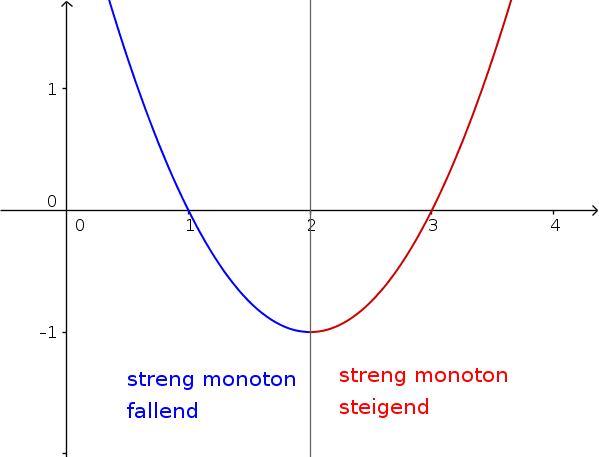
• monoton steigend, wenn $f(x_1)\le f(x_2)$
• monoton fallend, wenn $f(x_1)\ge f(x_2)$
• streng monoton steigend, wenn $f(x_1)< f(x_2)$
• streng monoton fallend, wenn $f(x_1)> f(x_2)$

Mit Hilfe der Ableitung lässt sich das Monotonieverhalten in einem Intervall bestimmen.

• monoton steigend, wenn für alle $x\in I$ gilt $f'(x)\ge0$
• monoton fallend, wenn für alle $x\in I$ gilt $f'(x)\le0$
• streng monoton steigend, wenn für alle $x\in I$ gilt $f'(x)>0$
• streng monoton fallend, wenn für alle $x\in I$ gilt $f'(x)<0$

Extrempunkte

Die Hoch- und Tiefpunkte eines Funktionsgraphen bezeichnet man als Extrempunkte. Als Voraussetzung, also notwendiges Kriterium, für das Vorhandensein eines Extrempunktes an der Stelle $x_E$ muss die erste Ableitung eine Nullstelle dort besitzen.

Zwar muss das Kriterium erfüllt sein, jedoch reicht dieses alleine nicht aus, um beurteilen zu können, ob nun wirklich ein Extrempunkt vorliegt und wenn ja, welche Art. Daher das hinreichende Kriterium, welches noch die zweite Ableitung einbezieht:

• Hochpunkt, wenn gilt $f''(x_E)<0$
• Tiefpunkt, wenn gilt $f''(x_E)>0$

Wendepunkte und Krümmungsverhalten

Als Krümmung bezeichnet man die Richtungsänderung eines Funktionsgraphen an einem Punkt (Wendepunkt).

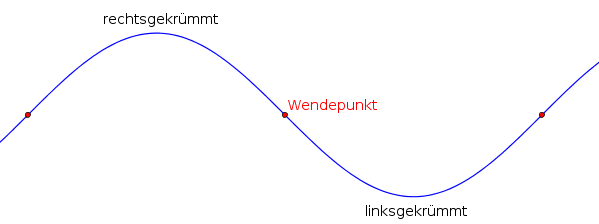
Um das Krümmungsverhalten zu bestimmen, sollte man zuerst die Wendestelle berechnen. Danach kann man die Krümmung auf den beiden Seiten des Wendepunktes bestimmen, indem man einen beliebigen Punkt links und einen rechts vom Wendepunkt in die zweite Ableitung einsetzt:

Die Funktion ist auf dem Intervall $I$ zweimal differenzierbar und

• linksgekrümmt, wenn für alle $x\in I$ gilt $f''(x)>0$
• rechtsgekrümmt, wenn für alle $x\in I$ gilt $f''(x)<0$