Lage von Kugeln und Ebenen

Es gibt ebenfalls drei mögliche Lagebeziehungen für eine Kugel und eine Ebene im Raum.

Um die Lage zu bestimmen, berechnet man den Abstand $d$ des Mittelpunktes der Kugel zur Ebene (siehe Abstand Punkt Ebene).

Der Abstand wird nun mit dem Radius $r$ verglichen.

$d>r$: keine gemeinsamen Punkte

$d=r$: gemeinsamer Berührpunkt

$d<r$: gemeinsamer Schnittkreis

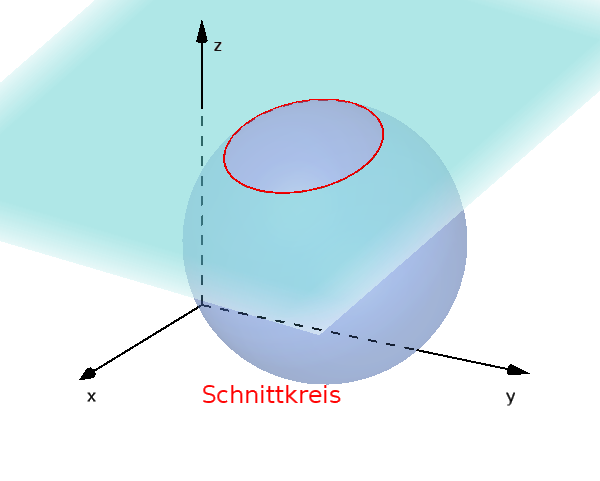
Schnittkreis berechnen

Beim 3. Fall lässt sich der Mittelpunkt $M'$ des Schnittkreises berechnen. Dazu stellt man folgende Geradengleichung auf.

$\vec{OM}$ ist der Mittelpunkt der Kugel und $\vec{n}$ ist der Normalenvektor der Ebene.

Der Schnittpunkt der Geraden $g$ und Ebene $E$ ist der Mittelpunkt des Kreises.

Zusätzlich kann auch der Radius $r'$ dieses Schnittkreises bestimmt werden.

Beispiel

$\text{E: } \left(\vec{x} - \begin{pmatrix} 5 \\4 \\ 3 \end{pmatrix}\right) \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}=0$

$k: (x+1)^2+(y-2)^2$ $+(z-1)^2=16$

1. Abstand von $M$ zu $E$

   Den Mittelpunkt der Kugel können wir aus der Kugelgleichung ablesen.

   $M(-1|2|1)$

   Wir berechnen den Abstand des Mittelpunktes $M$ zur Ebene $E$. Zuerst stellen wir die Hessesche Normalform (HNF) auf.

   $|\vec{n}|=\left|\begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}\right|$ $=1$

   Da der Betrag 1 ist, handelt es sich bereits um einen Normaleneinheitsvektor. Die HNF liegt also bereits vor.

   $\left(\vec{x} - \begin{pmatrix} 5 \\4 \\ 3 \end{pmatrix}\right) \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}=0$

   Der Mittelpunkt muss nun zur Abstandsberechnung nur noch eingesetzt werden.

   $d=\left|\left(\begin{pmatrix} -1 \\ 2 \\ 1 \end{pmatrix} - \begin{pmatrix} 5 \\4 \\ 3 \end{pmatrix}\right) \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}\right|$

   $d=\left|\begin{pmatrix} -6 \\ 8 \\ -2 \end{pmatrix} \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}\right|$

   $d=\left|0+0-2\right|$ $=|-2|$ $=2$

2. Bedingung überprüfen

   Zuerst liest man noch den Radius aus der Kugelgleichung ab.

   $r=\sqrt{16}=4$

   Wir schauen nun welcher der drei Fälle vorliegt.

   $2<4$

   $d<r$

   Der Abstand ist kleiner als der Radius ($d<r$), die Ebene liegt in der Kugel und es gibt daher einen Schnittkreis.

3. Gerade $g$ aufstellen und Schnittpunkt mit $E$

   Jetzt geht es darum, den neuen Mittelpunkt des Schnittkreises zu berechnen. Dazu wird wie oben beschrieben eine Geradengleichung aufgestellt.

   $g: \vec{x} = \vec{OM} + t \cdot \vec{n}$

   $g: \vec{x} = \begin{pmatrix} -1 \\ 2 \\ 1 \end{pmatrix} + t \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}$

   Der Schnittpunkt von der Geraden und der Ebene entspricht dem Mittelpunkt $M'$.

   Die Geradengleichung wird für $\vec{x}$ in die Ebene eingesetzt.

   $(\begin{pmatrix} -1 \\ 2 \\ 1 \end{pmatrix}$ $+ t \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}$ $- \begin{pmatrix} 5 \\4 \\ 3 \end{pmatrix}) \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}=0$

   
   

   $\begin{pmatrix} -6 \\ -2 \\ t-2 \end{pmatrix} \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}=0$

   $0+0+1\cdot(t-2)=0$
   $t-2=0\quad|+2$
   $t=2$

   Den Mittelpunkt $M'$ erhält man, indem das berechnete $t$ in die Geradengleichung eingesetzt wird.

   $\vec{OM'} = \begin{pmatrix} -1 \\ 2 \\ 1 \end{pmatrix} + 2 \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}$ $=\begin{pmatrix} -1 \\ 2 \\ 3 \end{pmatrix}$

   $M'(-1|2|3)$

4. Radius $r'$ berechnen

   Schließlich noch den Radius des Schnittkreises berechnen.

   Dazu setzt man das zuvor berechnete $d$ und den abgelesenen Radius $r$ der Kugel in folgende Formel ein:

   $r'=\sqrt{r^2-d^2}$

   $r'=\sqrt{4^2-2^2}$ $=\sqrt{12}$ $\approx3,46$

   Der Schnittkreis hat den Mittelpunkt $M'(-1|2|3)$ und den Radius $r\approx3,46$