Относительное положение сфер и плоскостей
Существует также три возможных соотношения для сферы и плоскости в трехмерном пространстве.
Запомните
Чтобы определить положение, вычислите расстояние $d$ от центра сферы до плоскости (смотрите расстояние точки плоскости).
Расстояние теперь сравнивается с радиусом $r$.
$d>r$: нет общих точек

$d=r$: общая точка
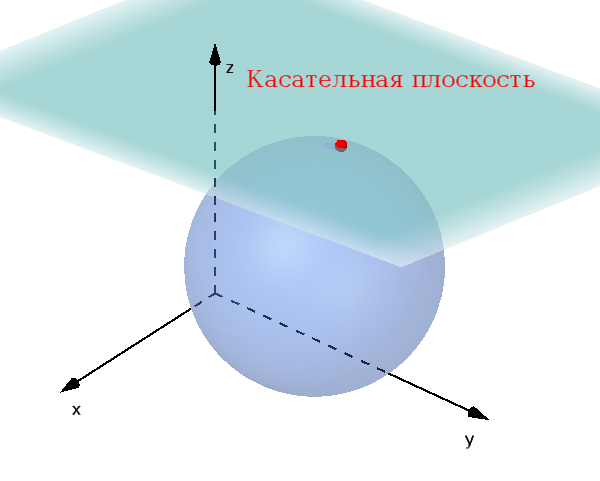
$d<r$: общий круг пересечения
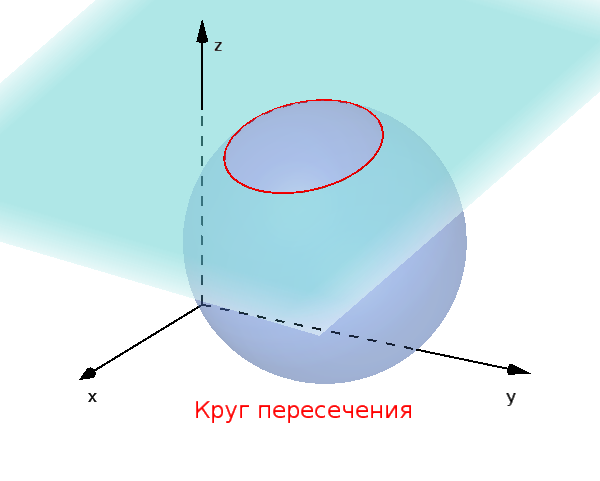
Информация
Вычислите круг пересечения
В третьем случае можно вычислить центр $M'$ окружности пересечения. Для этого необходимо задать следующее уравнение прямой.
$\vec{OM}$ является центром сферы и $\vec{n}$ является нормальным вектором плоскости.
Пересечение прямой $g$ и плоскости $E$ - это центр круга.
Кроме того, радиус $r'$ из этого круга пересечения также можно определить.
Метод
- Расстояние от $M$ до $E$
- Проверьте $r$ и $d$ (3 условия, см. выше)
- $M'$: Составьте $g$ и точки пересечения с $E$
- Вычислите радиус $r'$
Например
$\text{E: } \left(\vec{x} - \begin{pmatrix} 5 \\4 \\ 3 \end{pmatrix}\right) \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}=0$
$k: (x+1)^2+(y-2)^2$ $+(z-1)^2=16$
-
Расстояние от $M$ до $E$
Мы можем считать от центра сферы из уравнения сферы.
$M(-1|2|1)$
Рассчитаем расстояние от центра $M$ до плоскости $E$. Сначала мы устанавливаем Hормальную формулу Гессе (НФГ).
$|\vec{n}|=\left|\begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}\right|$ $=1$
Так как абсолютное значение равно 1, то это уже единичный нормальный вектор. У нас уже есть НФГ.
$\left(\vec{x} - \begin{pmatrix} 5 \\4 \\ 3 \end{pmatrix}\right) \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}=0$
Теперь центральная точка должна быть вставлена только для расчета расстояния.
$d=\left|\left(\begin{pmatrix} -1 \\ 2 \\ 1 \end{pmatrix} - \begin{pmatrix} 5 \\4 \\ 3 \end{pmatrix}\right) \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}\right|$
$d=\left|\begin{pmatrix} -6 \\ 8 \\ -2 \end{pmatrix} \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}\right|$
$d=\left|0+0-2\right|$ $=|-2|$ $=2$
-
Проверьте состояние
Сначала вы считываете радиус из уравнения сферы.
$r=\sqrt{16}=4$
Теперь мы рассмотрим, какой из трех случаев присутствует.
$2<4$
$d<r$
Расстояние меньше радиуса ($d<r$), плоскость лежит в сфере и поэтому существует круг пересечения.
-
Настройте прямую $g$ и точки пересечения с $E$
Теперь речь идет о вычислении нового центра круга пересечения. Уравнение прямой составляется так, как описано выше.
$g: \vec{x} = \vec{OM} + t \cdot \vec{n}$
$g: \vec{x} = \begin{pmatrix} -1 \\ 2 \\ 1 \end{pmatrix} + t \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}$
Пересечение прямой и плоскости соответствует центру $M'$.
Уравнение прямой вставляется для $\vec{x}$ в плоскость.
$(\begin{pmatrix} -1 \\ 2 \\ 1 \end{pmatrix}$ $+ t \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}$ $- \begin{pmatrix} 5 \\4 \\ 3 \end{pmatrix}) \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}=0$
$\begin{pmatrix} -6 \\ -2 \\ t-2 \end{pmatrix} \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}=0$
$0+0+1\cdot(t-2)=0$
$t-2=0\quad|+2$
$t=2$Центр $M'$ получается путем вставки вычисленного значения $t$ в уравнение прямой.
$\vec{OM'} = \begin{pmatrix} -1 \\ 2 \\ 1 \end{pmatrix} + 2 \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}$ $=\begin{pmatrix} -1 \\ 2 \\ 3 \end{pmatrix}$
$M'(-1|2|3)$
-
Вычислите радиус $r'$
Наконец, вычислите радиус круга пересечения.
Для этого вставьте предварительно вычисленный $d$ и считанный радиус $r$ сферы в следующую формулу::
$r'=\sqrt{r^2-d^2}$
$r'=\sqrt{4^2-2^2}$ $=\sqrt{12}$ $\approx3.46$
Круг пересечения имеет центр $M'(-1|2|3)$ и радиус $r\approx3.46$
