Относительное положение прямой и плоскости
Различаются три возможных относительных положения между прямой $g$ и плоскостью $E$.
- $g$ и $E$ пересекаются
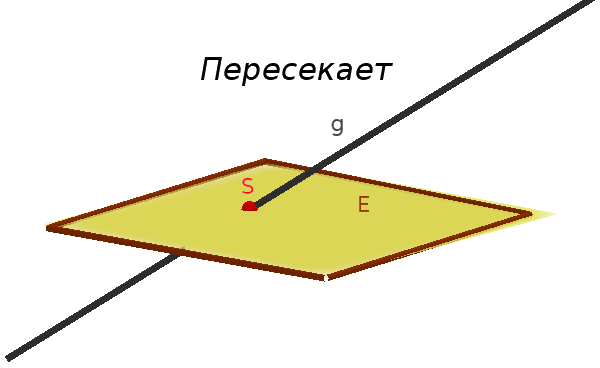
- $g$ и $E$ параллельны
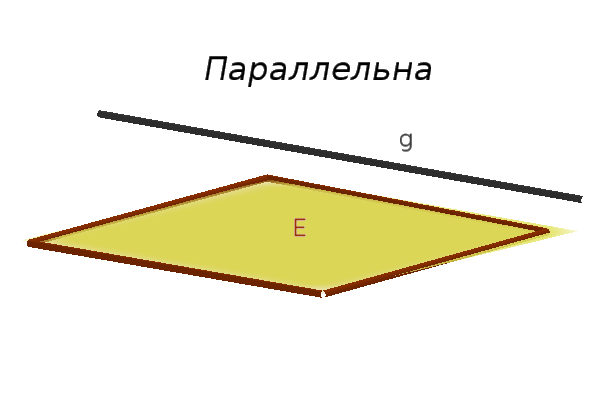
- $g$ прямая в плоскости $E$
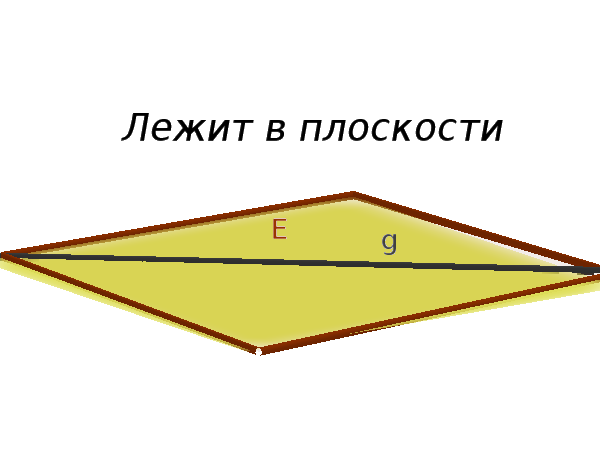
Запомните
- точное пересечение: $g$ и $E$ пересекаются
(пересечение) - неверное утверждение (например, $0=5$): $g$ параллельна $E$
(нет пересечения) -
истинное утверждение ( $5=5$): $g$ находится в $E$
(бесконечные пересечения)
Подсказка
Метод
- Перепишите уравнение прямой
- Вставьте $x$, $y$, $z$ в декартово уравнение плоскости и решите
- Интерпретируйте результаты
Например
$\text{g: } \vec{x} = \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ -3 \\ 4 \end{pmatrix}$
$\text{E: } 2x+y+2z=-2$
-
Перепишите уравнение прямой
Вектор $\vec{x}$ в уравнении прямой заменяется на $\begin{pmatrix} x \\ y \\ z \end{pmatrix}$.$\begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ -3 \\ 4 \end{pmatrix}$
Каждая строка соответствует уравнению
- $x=\color{red}{2+2r}$
- $y=\color{blue}{1-3r}$
- $z=\color{green}{1+4r}$
-
Вставьте $x$, $y$, $z$
Отдельные уравнения для $x$, $y$, $z$ могут быть вставлены в декартово уравнение плоскости.$\text{E: } 2\color{red}{x}+\color{blue}{y}+2\color{green}{z}=-2$
$2\cdot\color{red}{(2+2r)}$ $+\color{blue}{(1-3r)}$ $+2\cdot\color{green}{(1+4r)}$ $=-2$
Теперь раскрываем скобки и преобразуем уравнение в $r$
$4+4r+1-3r+2+8r$ $=-2$
$7+9r=-2\quad|-7$
$9r=-9\quad|:9$
$r=-1$ -
Интерпретируйте результаты
С тех пор как мы получили точный $r$, плоскость и прямая должны пересекаться, и вы можете вычислить пересечение.=> Прямая $g$ и плоскость $E$ пересекаются.
Пересечение вычисляется путем вставки $r=-1$ в уравнение прямой.
$\begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} + (-1) \cdot \begin{pmatrix} 2 \\ -3 \\ 4 \end{pmatrix}$ $=\begin{pmatrix} 0 \\ 4 \\ -3 \end{pmatrix}$
=> пересечение $S(0|4|-3)$.
