Относительное положение плоскости и плоскости

Различают три возможных относительных положения между двумя плоскостями $E$ и $F$.

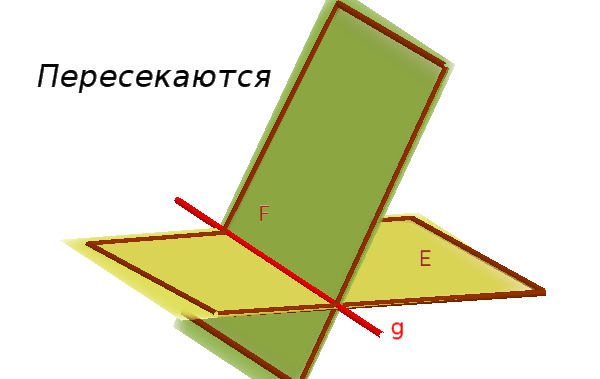
• Они пересекаются.
  
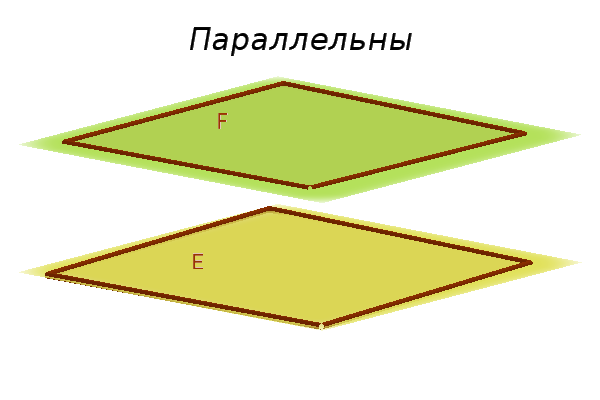
• Они параллельны.
  
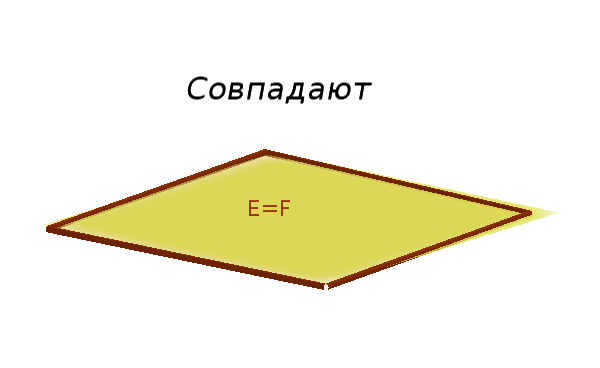
• Они совпадают.
  

Аналогично относительному положению прямых и плоскостей, можно попытаться вычислить прямую пересечения.
Однако, если вы сталкиваетесь с истинным утверждением (например, 0 = 0), плоскости совпадают. Если это утверждение неверно (например, 8 = 0), они параллельны.

Например

$\text{E: } x-y+z=2$

$\text{F: } 2x+y+z=4$

1. Составьте систему уравнений

   Эти два уравнения можно рассматривать как систему уравнений.
   1. $x-y+z=2$
   2. $2x+y+z=4$

   Теперь вы должны исключить переменную. Это достигается здесь, например, путем добавления двух уравнений.

   I.+II.

   $3x+2z=6$

2. Замените переменную на $r$

   Одна из других переменных теперь заменяется на $r$ и вставляется в уравнение. Например x:

   $\color{red}{x=r}$

   $3r+2z=6$

   Другая переменная ($z$) теперь может быть выражена как функция от $r$. Простое решение уравнение для $z$.

   $3r+2z=6\quad|-3r$
   $2z=6-3r\quad|:2$
   $\color{red}{z=3-1.5r}$

   Одно из двух уравнений плоскости также может быть использовано для определения $y$ с помощью $x$ и $z$.

   $x-y+z=2$
   $r-y+(3-1.5r)=2$
   $-0.5r-y+3=2\quad|+y$
   $-0.5r+3=2+y\quad|-2$
   $\color{red}{y=-0.5r+1}$

3. Составьте уравнение прямой

   Сначала мы пишем результаты для $x$, $y$ и $z$ между собой.
   1. $x=r$
   2. $y=-0.5r+1$
   3. $z=3-1.5r$

   Упорядочивание:

   1. $x=\color{blue}{0}\color{green}{+1}r$
   2. $y=\color{blue}{1}\color{green}{-0.5}r$
   3. $z=\color{blue}{3}\color{green}{-1.5}r$

   Теперь это можно легко представить в виде уравнения прямой.

   $\vec{x} = \begin{pmatrix} \, \\ \, \\ \, \end{pmatrix} + r \cdot \begin{pmatrix} \, \\ \, \\ \, \end{pmatrix}$

   $\vec{x} = \begin{pmatrix} \color{blue}{0} \\ \color{blue}{1} \\ \color{blue}{3} \end{pmatrix} + r \cdot \begin{pmatrix} \color{green}{1} \\ \color{green}{-0.5} \\ \color{green}{-1.5} \end{pmatrix}$

Например (параллельно)

$\text{E: } x-y+z=2$

$\text{F: } 2x-2y+2z=7$

1. Составьте систему уравнений

   1. $x-y+z=2\,\,\,|\cdot(-2)$
   2. $2x-2y+2z=7$

   Мы применяем метод сложения.

   1. $-2x+2y-2z=-4$
   2. $2x-2y+2z=7$

   I.+II.
   $0=3$ f. s.

2. Интерпретируйте результаты

   Мы получаем противоречие или ложное утверждение.

   $0\neq3$

   $E$ и $F$ не имеют общей точки. Плоскости должны быть параллельными.

   => $E$ и $F$ параллельны