Трехмерные линии
Существуют также линии в трехмерном пространстве. Однако, их уравнение отличается от уравнения линейной функции.
Вместо наклона у вас есть вектор направления в пространстве. Прямые имеют определенное положение (в отличии от векторов).
!
Запомните
Прямая определяется точкой и вектором направления.
Параметрическое уравнение прямой
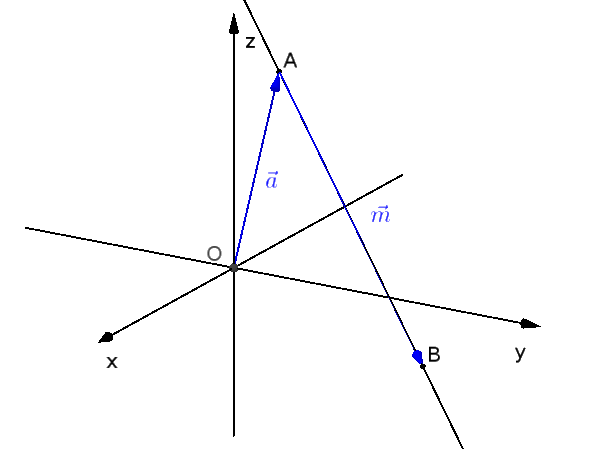
Параметрическим уравнением прямой, является формула:
$\text{g: } \vec{x} = \vec{a} + r \cdot \vec{m}$
$\text{g: } \vec{x} = \vec{OA} + r \cdot \vec{AB}$
Уравнение состоит из:
- вектора опоры: это вектор положения любой точки на прямой.
- вектор направления, он определяет направление линии.
i
Информация
Коэффициент $r$ перед вектором направления равен скалярному произведению.
Это означает, что вектор направления может быть продлен произвольно (на $r$), так как прямая с обеих сторон уходит в бесконечность.
