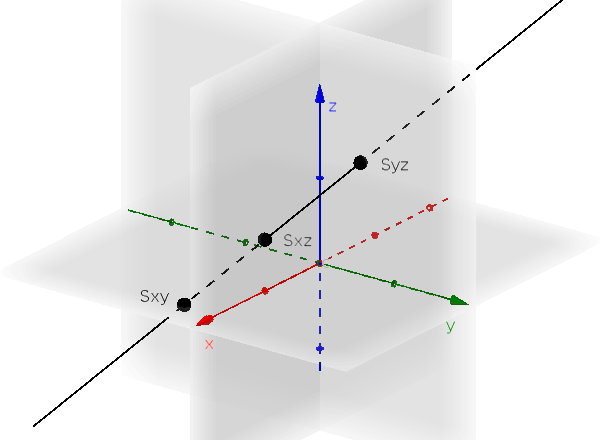
Пересечения
Пересечение прямой с координатными плоскостями $E_{xy}$, $E_{xz}$, $E_{yz}$ называют пересечениями.
Запомните
Метод
- Установите соответствующую координату равной нулю и определите $r$
- Вставьте $r$ в линейное уравнение, чтобы получить пересечения
Подсказка
- $E_{xy}: z=0$
- $E_{xz}: y=0$
- $E_{yz}: x=0$
Например
Определите пересечение прямой $g$ с плоскостью xy.
$\text{g: } \vec{x} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + r \cdot \begin{pmatrix} 4 \\ 5 \\ 6 \end{pmatrix}$
-
Определите $r$
Поскольку это плоскость $E_{xy}$, мы устанавливаем z равным 0.$\begin{pmatrix} x \\ y \\ 0 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + r \cdot \begin{pmatrix} 4 \\ 5 \\ 6 \end{pmatrix}$
Строка, содержащая только одну переменную (третья), должна быть решена для $r$.
$0=3+6r\quad|-3$
$-3=6r\quad|:6$
$r=-0.5$ -
Определите пересечение
$\text{g: } \vec{x} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + r \cdot \begin{pmatrix} 4 \\ 5 \\ 6 \end{pmatrix}$
Рассчитанное значение $r=-0.5$, используется в линейном уравнении.
$\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + (-0.5) \cdot \begin{pmatrix} 4 \\ 5 \\ 6 \end{pmatrix}$ $=\begin{pmatrix} -1 \\ -0.5 \\ 0 \end{pmatrix}$
Пересечение с плоскостью XY находится в точке $S_{xy}(-1|-0.5|0)$
