Intercepts

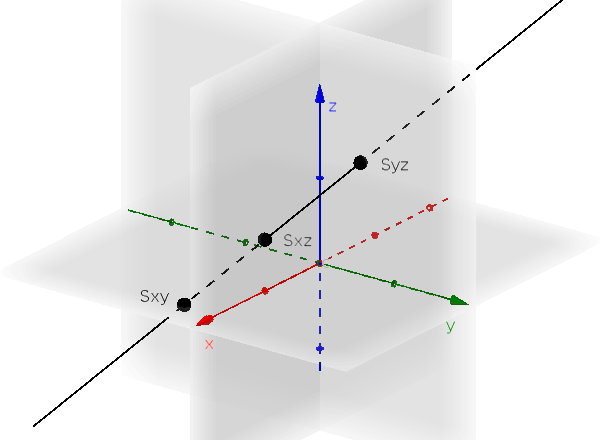
The intersections of a line with the coordinate planes $E_{xy}$, $E_{xz}$, $E_{yz}$ are called intercepts.

Example

Determine the intercept of the line $g$ with the xy-plane.

$\text{g: } \vec{x} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + r \cdot \begin{pmatrix} 4 \\ 5 \\ 6 \end{pmatrix}$

1. Determine $r$

   Since it is the plane $E_{xy}$, we set z equal to 0.

   $\begin{pmatrix} x \\ y \\ 0 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + r \cdot \begin{pmatrix} 4 \\ 5 \\ 6 \end{pmatrix}$

   The row with just one variable (the third) has to be solved for $r$.

   $0=3+6r\quad|-3$
   $-3=6r\quad|:6$
   $r=-0.5$

2. Determine intercept

   $\text{g: } \vec{x} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + r \cdot \begin{pmatrix} 4 \\ 5 \\ 6 \end{pmatrix}$

   The calculated $r=-0.5$ is used in the linear equation.

   $\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + (-0.5) \cdot \begin{pmatrix} 4 \\ 5 \\ 6 \end{pmatrix}$ $=\begin{pmatrix} -1 \\ -0.5 \\ 0 \end{pmatrix}$

   The intercept with the xy-plane is at $S_{xy}(-1|-0.5|0)$