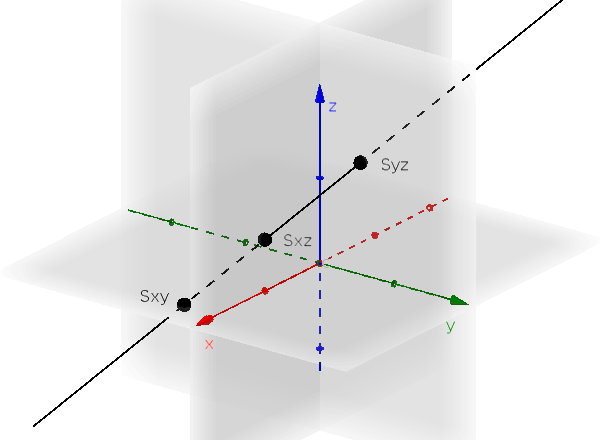
Spurpunkte
Die Schnittpunkte der Geraden mit den Koordinatenebenen $E_{xy}$, $E_{xz}$, $E_{yz}$ nennt man Spurpunkte.
Merke
Vorgehensweise
- Entsprechende Koordinate gleich Null setzen und $r$ berechnen
- $r$ in die Geradengleichung einsetzen, um Spurpunkt zu erhalten
Tipp
- $E_{xy}: z=0$
- $E_{xz}: y=0$
- $E_{yz}: x=0$
Beispiel
Berechne den Spurpunkt der Geraden $g$ mit der xy-Ebene.
$\text{g: } \vec{x} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + r \cdot \begin{pmatrix} 4 \\ 5 \\ 6 \end{pmatrix}$
-
$r$ berechnen
Da es sich um die Ebene $E_{xy}$ handelt, setzen wir z gleich 0.$\begin{pmatrix} x \\ y \\ 0 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + r \cdot \begin{pmatrix} 4 \\ 5 \\ 6 \end{pmatrix}$
Die Zeile mit nur einer Variablen (hier die dritte) wird nach $r$ umgestellt.
$0=3+6r\quad|-3$
$-3=6r\quad|:6$
$r=-0,5$ -
Spurpunkt bestimmen
$\text{g: } \vec{x} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + r \cdot \begin{pmatrix} 4 \\ 5 \\ 6 \end{pmatrix}$
Das berechnete $r=-0,5$ wird in die Geradengleichung eingesetzt.
$\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + (-0,5) \cdot \begin{pmatrix} 4 \\ 5 \\ 6 \end{pmatrix}$ $=\begin{pmatrix} -1 \\ -0,5 \\ 0 \end{pmatrix}$
Der Spurpunkt mit der xy-Ebene ist $S_{xy}(-1|-0,5|0)$
