Geraden im Raum
Auch im dreidimensionalen Raum gibt es Geraden. Deren Gleichung sieht jedoch anders aus als bei linearen Funktionen.
Anstatt einer Steigung hat man im Raum einen Richtungsvektor. Geraden haben (im Gegensatz zu Vektoren) eine eindeutige Lage.
!
Merke
Eine Gerade ist durch einen Punkt und einen Richtungsvektor eindeutig definiert.
Parametergleichung einer Geraden
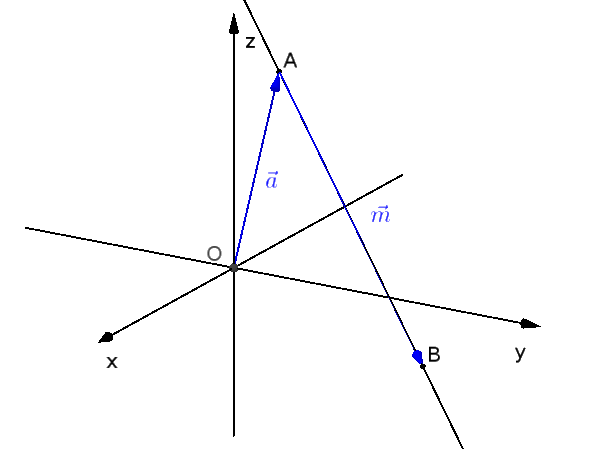
Die Parametergleichung einer Geraden lautet:
$\text{g: } \vec{x} = \vec{a} + r \cdot \vec{m}$
$\text{g: } \vec{x} = \vec{OA} + r \cdot \vec{AB}$
Die Gleichung besteht aus
- einem Stützvektor: Dabei handelt es sich um den Ortsvektor eines beliebigen Punktes (dem Stützpunkt) auf der Geraden.
- dem Richtungsvektor, der die Richtung der Geraden bestimmt.
i
Info
Bei dem Faktor $r$ vor dem Richtungsvektor handelt es sich um Skalarmultplikation.
Das bedeutet, der Richtungsvektor kann beliebig (um $r$) verlängert werden, da die Gerade auf beiden Seiten ins Unendliche geht.
