Skalarmultiplikation
Skalarmultiplikation meint die Multiplikation eines Vektors mit einer reellen Zahl $s$.
$s\cdot\vec{a}$ $=s\cdot\begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix}$ $=\begin{pmatrix}s\cdot a_1\\s\cdot a_2\\s\cdot a_3\end{pmatrix}$
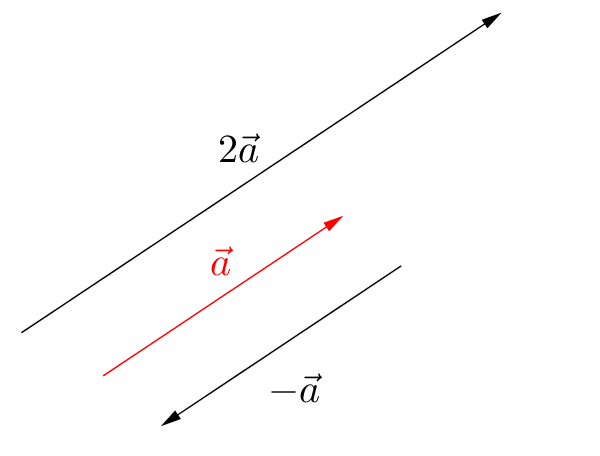
Bei der Skalarmultiplikation erhält man einen parallelen Vektor. Dabei ändert der Vektor (bei $|s|\neq1$) seine Länge und bei $s<0$ zeigt er in die entgegengesetze Richtung.
!
Merke
Für $s=-1$ erhält man den sogenannten Gegenvektor $-\vec{a}$.
Dieser ist in der Länge identisch mit $\vec{a}$ und zeigt nur in die entgegengesetzte Richtung.
Dieser ist in der Länge identisch mit $\vec{a}$ und zeigt nur in die entgegengesetzte Richtung.
Beispiel
$3\cdot\begin{pmatrix}4\\2\\3\end{pmatrix}$ $=\begin{pmatrix}3\cdot4\\3\cdot2\\3\cdot3\end{pmatrix}$ $=\begin{pmatrix}12\\6\\9\end{pmatrix}$
!
Merke
Bei der Skalarmultiplikation gilt das Distributivgesetz.
$r\cdot(\vec{a}+\vec{b})=r\cdot\vec{a}+r\cdot\vec{b}$
$(r+s)\cdot\vec{a}=r\cdot\vec{a}+s\cdot\vec{a}$
$r, s \in\mathbb{R}$
$r\cdot(\vec{a}+\vec{b})=r\cdot\vec{a}+r\cdot\vec{b}$
$(r+s)\cdot\vec{a}=r\cdot\vec{a}+s\cdot\vec{a}$
$r, s \in\mathbb{R}$
