Kreuzprodukt
Neben dem Skalarprodukt gibt es noch das Kreuzprodukt oder Vektorprodukt zweier Vektoren. Das Ergebnis ist dann ein Vektor, der senkrecht auf den beiden anderen steht.
Mathematisch lässt sich das Kreuzprodukt so berechnen:
$\vec{a}\times\vec{b}$ $=\begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix}\times\begin{pmatrix}b_1\\b_2\\b_3\end{pmatrix}$
$=\begin{pmatrix}a_2\cdot b_3-a_3\cdot b_2\\a_3\cdot b_1-a_1\cdot b_3\\a_1\cdot b_2- a_2\cdot b_1\end{pmatrix}$
i
Info
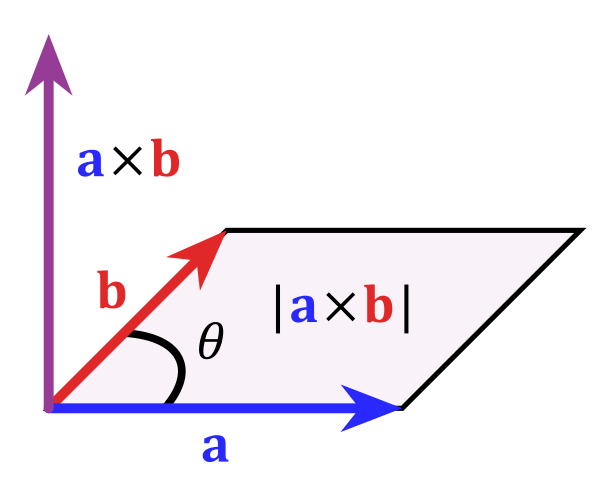
Der Betrag des Vektors $\vec{c}=\vec{a}\times\vec{b}$ entspricht dem Flächeninhalt des von $\vec{a}$und $\vec{b}$ aufgespannten Parallelogramms.
$A=|\vec{c}|$ $=|\vec{a}\times\vec{b}|$
$A=|\vec{c}|$ $=|\vec{a}\times\vec{b}|$
i
Tipp
Das Kreuzprodukt ist häufig eine schnelle Alternative, um einen Normalenvektor für eine Normalengleichung zu berechnen.
Da die Formel jedoch schwer zu merken ist, wird sie manchmal nicht unterrichtet.
Da die Formel jedoch schwer zu merken ist, wird sie manchmal nicht unterrichtet.
Beispiel
$\begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix}\times\begin{pmatrix}b_1\\b_2\\b_3\end{pmatrix}$ $=\begin{pmatrix}a_2\cdot b_3-a_3\cdot b_2\\a_3\cdot b_1-a_1\cdot b_3\\a_1\cdot b_2- a_2\cdot b_1\end{pmatrix}$
$\begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix} \times\begin{pmatrix} 1 \\ 5 \\ 2 \end{pmatrix}$ $=\begin{pmatrix} 1\cdot2 - 0\cdot5 \\ 0\cdot1 - 1\cdot2 \\ 1\cdot5 - 1\cdot1 \end{pmatrix}$ $=\begin{pmatrix} 2 \\ -2 \\ 4 \end{pmatrix}$
Kreuzprodukt Vektoren berechnen, Normalenvektor, Vektorprodukt, Normalenvektor Parameterform
Kooperation mit dem Kanal von Mister Mathe

