Cross product
In addition to the scalar product, there is the cross product (or vector product) of two vectors. As a result you get a vector that is perpendicular to the other vectors.
Mathematically, the cross product can be calculated as follows:
$\vec{a}\times\vec{b}$ $=\begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix}\times\begin{pmatrix}b_1\\b_2\\b_3\end{pmatrix}$
$=\begin{pmatrix}a_2\cdot b_3-a_3\cdot b_2\\a_3\cdot b_1-a_1\cdot b_3\\a_1\cdot b_2- a_2\cdot b_1\end{pmatrix}$
i
Info
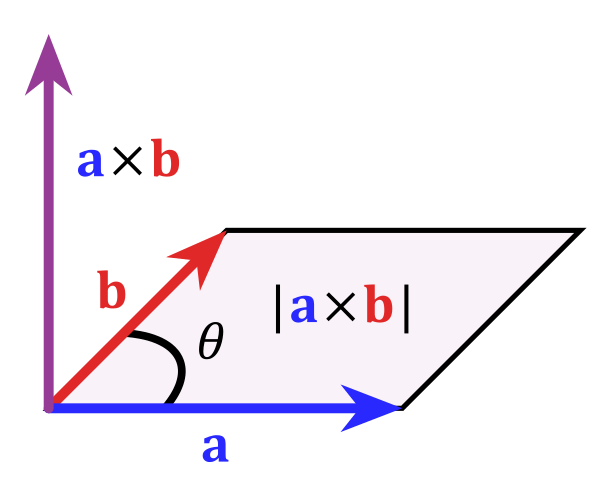
The magnitude of the vector $\vec{c}=\vec{a}\times\vec{b}$ equals the surface area of the parallelogram formed by $\vec{a}$ and $\vec{b}$.
$A=|\vec{c}|$ $=|\vec{a}\times\vec{b}|$
$A=|\vec{c}|$ $=|\vec{a}\times\vec{b}|$
i
Hint
The cross product is often a quick alternative to calculate a normal vector for a normal equation.
However, this formula is hard to memorize so sometimes it is not taught in school.
However, this formula is hard to memorize so sometimes it is not taught in school.
Example
$\begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix}\times\begin{pmatrix}b_1\\b_2\\b_3\end{pmatrix}$ $=\begin{pmatrix}a_2\cdot b_3-a_3\cdot b_2\\a_3\cdot b_1-a_1\cdot b_3\\a_1\cdot b_2- a_2\cdot b_1\end{pmatrix}$
$\begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix} \times\begin{pmatrix} 1 \\ 5 \\ 2 \end{pmatrix}$ $=\begin{pmatrix} 1\cdot2 - 0\cdot5 \\ 0\cdot1 - 1\cdot2 \\ 1\cdot5 - 1\cdot1 \end{pmatrix}$ $=\begin{pmatrix} 2 \\ -2 \\ 4 \end{pmatrix}$
