Linear combination
A linear combination of vectors is the addition of vectors, which are multiplied by a real number (scalar multiplication). This creates a new vector.
$\vec{v}=r_1\cdot\vec{a_1}+r_2\cdot\vec{a_2}+$ $...+r_n\cdot\vec{a_n}$
Collinear vectors
Two vectors with parallel arrows are called collinear. One vector can then be represented as a linear combination of the other.

$\vec{a}=r\cdot\vec{b}$ or $\vec{b}=r\cdot\vec{a}$
Coplanar vectors
Vectors that can be depicted in the same plane are coplanar. In that case, each vector can be depicted as a linear combination of the other one.
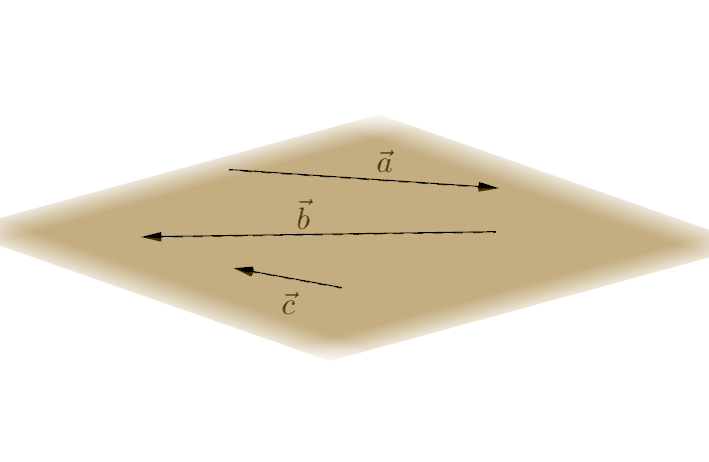
$\vec{a}=r\cdot\vec{b}+s\cdot\vec{c}$ or
$\vec{b}=r\cdot\vec{a}+s\cdot\vec{c}$ or
$\vec{c}=r\cdot\vec{a}+s\cdot\vec{b}$
$\vec{b}=r\cdot\vec{a}+s\cdot\vec{c}$ or
$\vec{c}=r\cdot\vec{a}+s\cdot\vec{b}$
