Scalar multiplication

Scalar multiplication describes the multiplication of a vector with a real number $s$.

$s\cdot\vec{a}$ $=s\cdot\begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix}$ $=\begin{pmatrix}s\cdot a_1\\s\cdot a_2\\s\cdot a_3\end{pmatrix}$

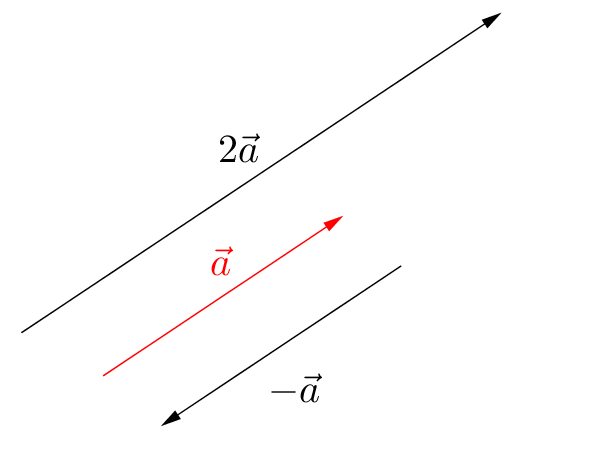
In scalar multiplication, one obtains a parallel vector. In this case, the vector (at $|s|\neq1$) changes its length and at $s<0$ it points in the opposite direction.

Remember

For $s=-1$ we get the so-called inverse vector $-\vec{a}$.
It has the same length as $\vec{a}$ but points in the opposite direction.

Example

$3\cdot\begin{pmatrix}4\\2\\3\end{pmatrix}$ $=\begin{pmatrix}3\cdot4\\3\cdot2\\3\cdot3\end{pmatrix}$ $=\begin{pmatrix}12\\6\\9\end{pmatrix}$

Remember

For scalar multiplication, the distributive law applies.
$r\cdot(\vec{a}+\vec{b})=r\cdot\vec{a}+r\cdot\vec{b}$
$(r+s)\cdot\vec{a}=r\cdot\vec{a}+s\cdot\vec{a}$

$r, s \in\mathbb{R}$