Addition und subtraction of vectors
The addition and subtraction of vectors is done component by component.
i
Info
Vectors of different dimensions (e.g. vectors in the plane and vectors of the three dimensional space) can not be added / subtracted.
Addition of vectors
$\vec{a}+\vec{b}$ $=\begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix}+\begin{pmatrix}b_1\\b_2\\b_3\end{pmatrix}$ $=\begin{pmatrix}a_1+b_1\\a_2+b_2\\a_3+b_3\end{pmatrix}$
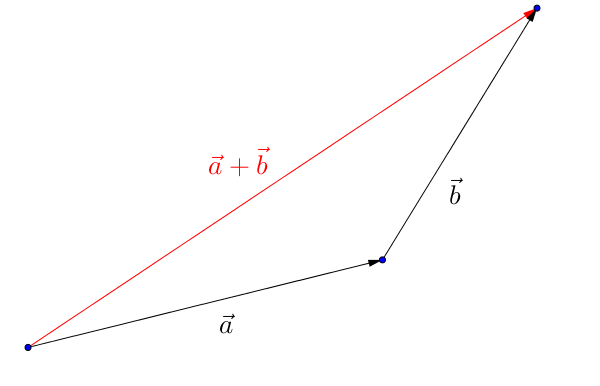
Geometrically interpreted, the arrows of the vectors are connected to each other.
!
Remember
The order of addition does not matter. The commutative law applies:
$\vec{a}+\vec{b}=\vec{b}+\vec{a}$
In addition, the associative law also applies:
$(\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})$
$\vec{a}+\vec{b}=\vec{b}+\vec{a}$
In addition, the associative law also applies:
$(\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})$
Subtraction of vectors
$\vec{a}-\vec{b}$ $=\begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix}-\begin{pmatrix}b_1\\b_2\\b_3\end{pmatrix}$ $=\begin{pmatrix}a_1-b_1\\a_2-b_2\\a_3-b_3\end{pmatrix}$
!
Remember
The subtraction of vectors is not commutative!
$\vec{a}-\vec{b}\neq\vec{b}-\vec{a}$
$\vec{a}-\vec{b}\neq\vec{b}-\vec{a}$
Examples
$\begin{pmatrix}2\\4\end{pmatrix}+\begin{pmatrix}1\\3\end{pmatrix}$ $=\begin{pmatrix}2+1\\4+3\end{pmatrix}$ $=\begin{pmatrix}3\\7\end{pmatrix}$
$\begin{pmatrix}1\\2\\3\end{pmatrix}+\begin{pmatrix}4\\5\\6\end{pmatrix}$ $=\begin{pmatrix}1+4\\2+5\\3+6\end{pmatrix}$ $=\begin{pmatrix}5\\7\\9\end{pmatrix}$
$\begin{pmatrix}4\\5\\6\end{pmatrix}-\begin{pmatrix}1\\2\\3\end{pmatrix}$ $=\begin{pmatrix}4-1\\5-2\\6-3\end{pmatrix}$ $=\begin{pmatrix}3\\3\\3\end{pmatrix}$
