Векторное произведение
В дополнение к скалярному произведению, существует векторное произведение (или перекрестное произведение) двух векторов. В результате вы получите вектор, перпендикулярный другим векторам.
Математически, векторное произведение можно вычислить по формуле:
$\vec{a}\times\vec{b}$ $=\begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix}\times\begin{pmatrix}b_1\\b_2\\b_3\end{pmatrix}$
$=\begin{pmatrix}a_2\cdot b_3-a_3\cdot b_2\\a_3\cdot b_1-a_1\cdot b_3\\a_1\cdot b_2- a_2\cdot b_1\end{pmatrix}$
i
Информация
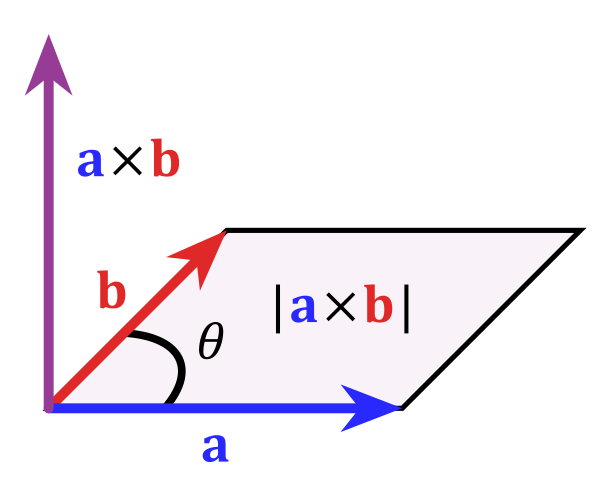
Величина вектора $\vec{c}=\vec{a}\times\vec{b}$ равна площади поверхности параллелограмма, образованного $\vec{a}$ и $\vec{b}$.
$A=|\vec{c}|$ $=|\vec{a}\times\vec{b}|$
$A=|\vec{c}|$ $=|\vec{a}\times\vec{b}|$
i
Подсказка
Векторное произведение зачастую является быстрой альтернативой, чтобы вычислить нормальный вектор для нормального уравнения.
Однако, эту формулу сложно запомнить, так что иногда она пропускается.
Однако, эту формулу сложно запомнить, так что иногда она пропускается.
Пример
$\begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix}\times\begin{pmatrix}b_1\\b_2\\b_3\end{pmatrix}$ $=\begin{pmatrix}a_2\cdot b_3-a_3\cdot b_2\\a_3\cdot b_1-a_1\cdot b_3\\a_1\cdot b_2- a_2\cdot b_1\end{pmatrix}$
$\begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix} \times\begin{pmatrix} 1 \\ 5 \\ 2 \end{pmatrix}$ $=\begin{pmatrix} 1\cdot2 - 0\cdot5 \\ 0\cdot1 - 1\cdot2 \\ 1\cdot5 - 1\cdot1 \end{pmatrix}$ $=\begin{pmatrix} 2 \\ -2 \\ 4 \end{pmatrix}$
