Lines in three dimensional space
There are also lines in three-dimensional space. However, their equation does not look like the equation of a linear function.
Instead of a slope, you have a direction vector in space. Lines have a definite position (as opposed to vectors).
!
Remember
A line is uniquely defined by a point and a direction vector.
Parametric equation of a line
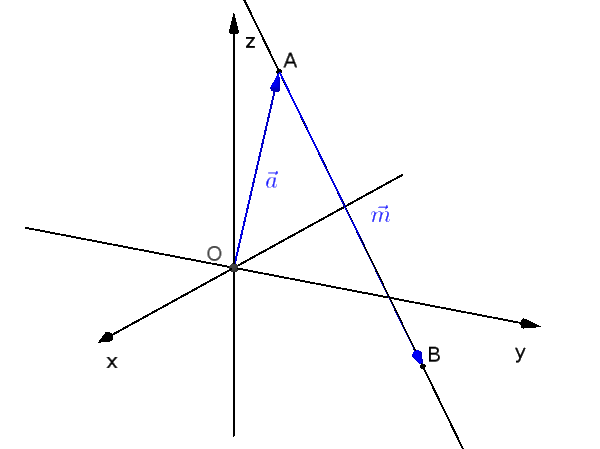
The parametric equation of a line is:
$\text{g: } \vec{x} = \vec{a} + r \cdot \vec{m}$
$\text{g: } \vec{x} = \vec{OA} + r \cdot \vec{AB}$
The equation consists of
- a support vector: This is the position vector of any point on the line.
- the direction vector that determines the direction of the line.
i
Info
The factor $r$ in front of the direction vector is about scalar multiplication.
This means that the direction vector can be extended arbitrarily (by $r$), since the line on both sides goes to infinity.
