Ortsvektor

Beim Ortsvektor $\overrightarrow{OP}$ eines Punktes $P(p_1|p_2)$ liegt der Anfangspunkt immer im Koordinatenursprung $O(0|0)$.
Die Koordinaten des Vektors entsprechen daher denen des Punktes.

$\overrightarrow{OP}=\begin{pmatrix}p_1\\p_2\end{pmatrix}$

Im dreidimensionalen Raum mit $P(p_1|p_2|p_3)$:

$\overrightarrow{OP}=\begin{pmatrix}p_1\\p_2\\p_3\end{pmatrix}$

Tipp

Der Ortsvektor ist ein Verbindungsvektor mit dem Ursprung als Anfangspunkt.

Beispiel

Ortsvektor $\overrightarrow{OP}$ von $P(3|2)$

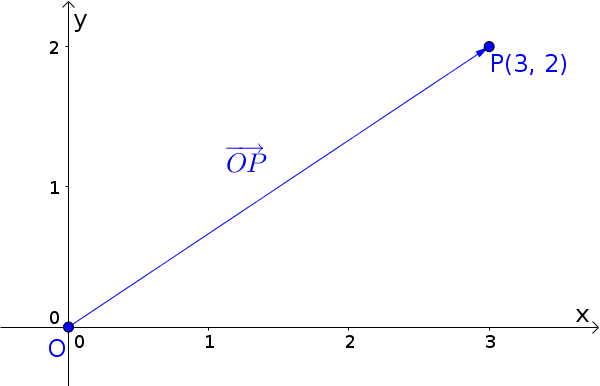
$\overrightarrow{OP}=\begin{pmatrix}3\\2\end{pmatrix}$