Verbindungsvektor
Einen Spaltenvektor, der den Anfangspunkt $P(p_1|p_2)$ und den Endpunkt $Q(q_1|q_2)$ verbindet, kann man wie folgt bestimmen:
$\overrightarrow{PQ}=\begin{pmatrix}q_1-p_1\\q_2-p_2\end{pmatrix}$
Und im Raum mit $P(p_1|p_2|p_3)$ und $Q(q_1|q_2|q_3)$:
$\overrightarrow{PQ}=\begin{pmatrix}q_1-p_1\\q_2-p_2\\q_3-p_3\end{pmatrix}$
!
Merke
Die Koordinaten des Verbindungsvektors von zwei Punkten entsprechen den Koordinatendifferenzen vom Endpunkt und Anfangspunkt.
Beispiel
Vektor $\overrightarrow{PQ}$ mit $P(1|3)$ und $Q(4|1)$
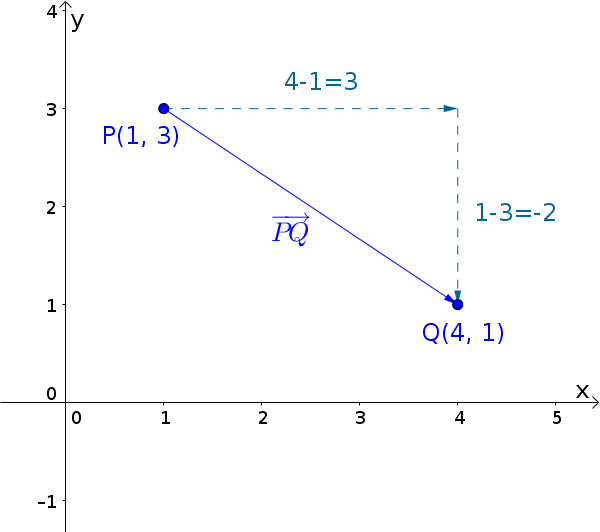
$\overrightarrow{PQ}=\begin{pmatrix}4-1\\1-3\end{pmatrix}=\begin{pmatrix}3\\-2\end{pmatrix}$
