Вектора между двумя точками
Вектор-столбец соединяет первоначальную точку $P(p_1|p_2)$ и конечную точку $Q(q_1|q_2)$, может быть определен как:
$\overrightarrow{PQ}=\begin{pmatrix}q_1-p_1\\q_2-p_2\end{pmatrix}$
В трехмерном пространстве с $P(p_1|p_2|p_3)$ и $Q(q_1|q_2|q_3)$:
$\overrightarrow{PQ}=\begin{pmatrix}q_1-p_1\\q_2-p_2\\q_3-p_3\end{pmatrix}$
!
Справка
Координаты вектора-столбца между двумя точками соответствуют разности координат конечной точки и первоначальной точки.
Пример
Вектор $\overrightarrow{PQ}$ с $P(1|3)$ и $Q(4|1)$
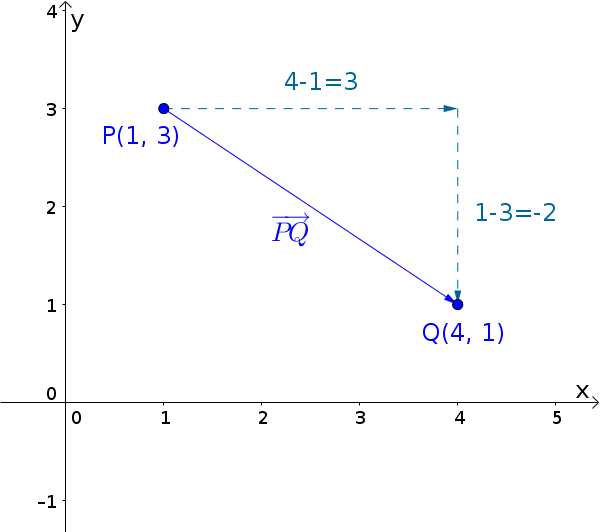
$\overrightarrow{PQ}=\begin{pmatrix}4-1\\1-3\end{pmatrix}=\begin{pmatrix}3\\-2\end{pmatrix}$
