Длина вектора
Для определения длины вектора $|\vec{v}|$ мы используем Теорему Пифагора.
Длина вектора $\vec{v}=\begin{pmatrix}v_1\\v_2\end{pmatrix}$ равняется:
$|\vec{v}|=\left|\begin{pmatrix}v_1\\v_2\end{pmatrix}\right|=\sqrt{v_1^2+v_2^2}$
В трехмерном пространстве:
$|\vec{v}|=\left|\begin{pmatrix}v_1\\v_2\\v_3\end{pmatrix}\right|=\sqrt{v_1^2+v_2^2+v_3^2}$
!
Запомни
Длина вектора - это длина его стрелки, соответствующая расстоянию между первоначальной и конечной точками.
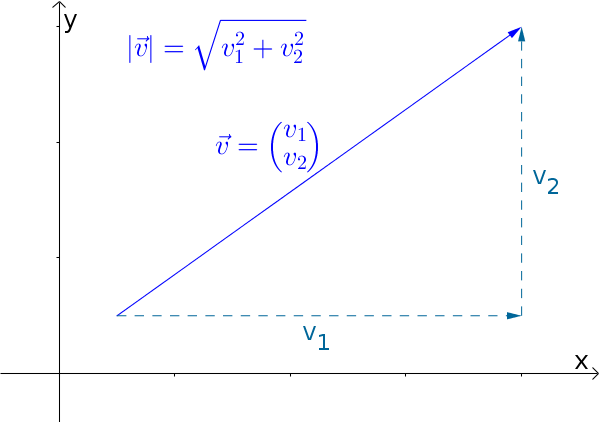
Для определения длины стрелки, подумайте о следующем треугольнике. При помощи Теоремы Пифагора, вы найдете длину стрелки.
Примеры
Определите длину вектора $\vec{a}=\begin{pmatrix}3\\4\end{pmatrix}$$|\vec{a}|=\sqrt{3^2+4^2}=\sqrt{25}=5$
Определите длину вектора $\vec{a}=\begin{pmatrix}2\\3\\6\end{pmatrix}$
$|\vec{a}|=\sqrt{2^2+3^2+6^2}=\sqrt{49}$ $=7$
