Math ↠ Relative position of planes ↠ Line and plane

Relative position of line and plane

A distinction is made between three possible relative positions between a line $g$ and a plane $E$.

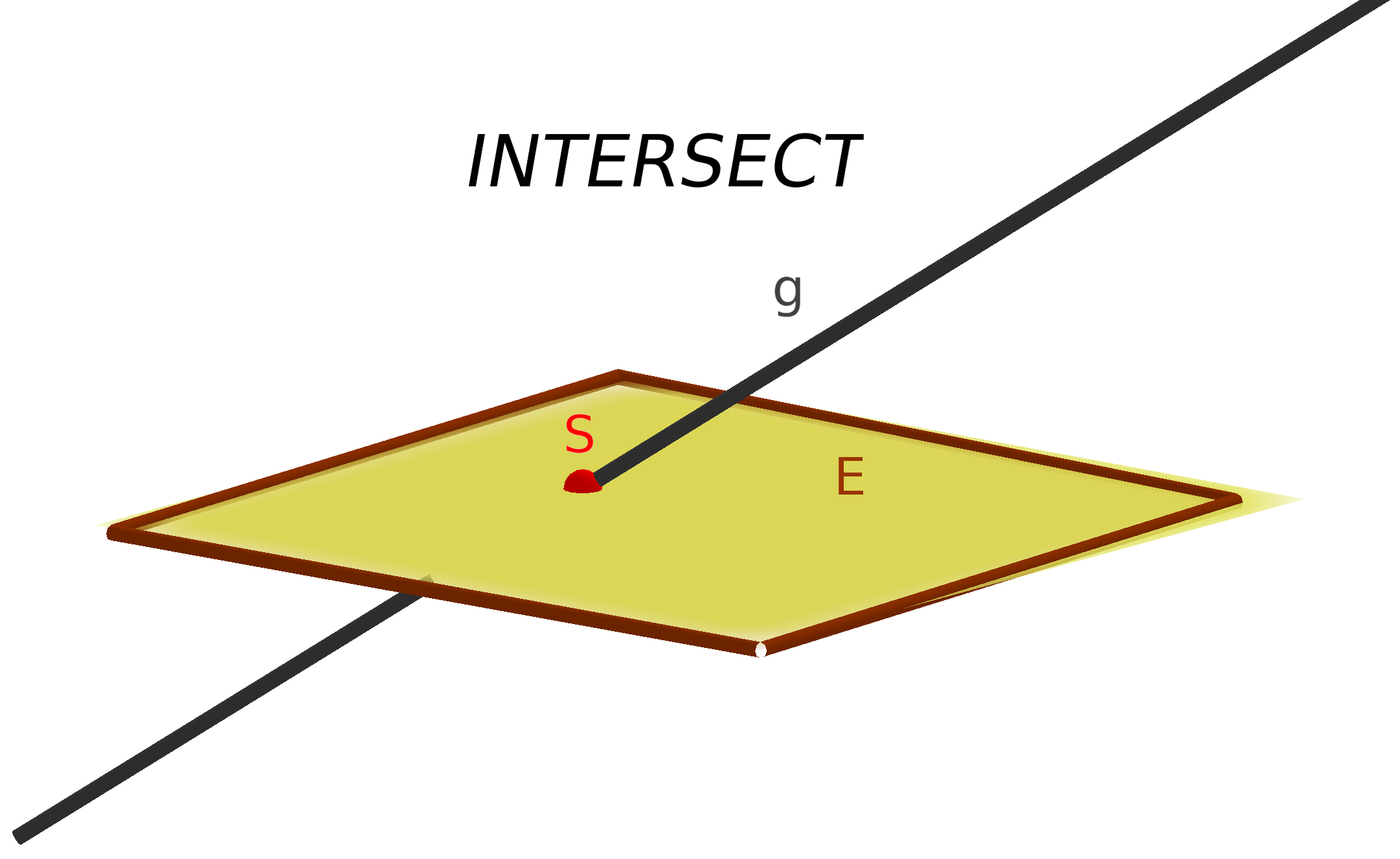
  • $g$ and $E$ intersect
    intersect
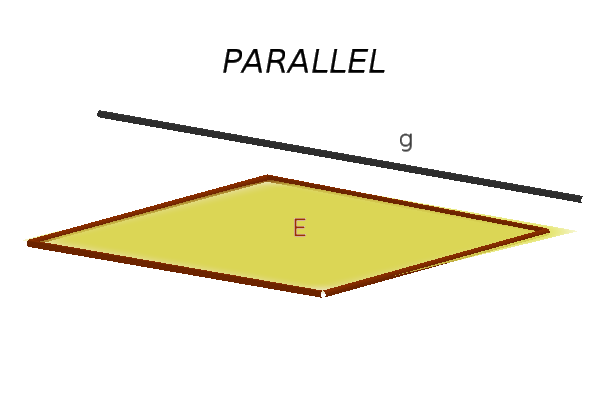
  • $g$ and $E$ are parallel
    parallel
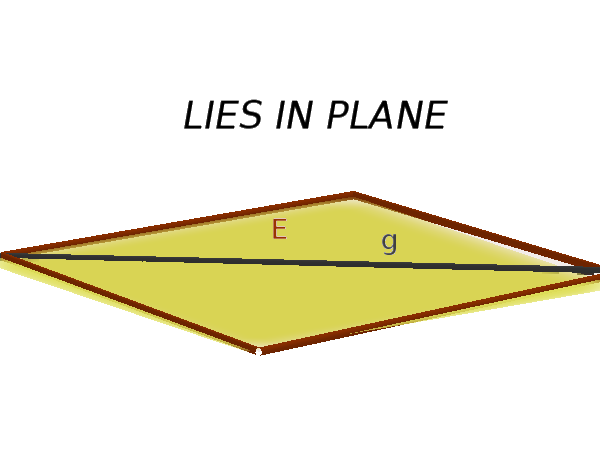
  • $g$ lies in plane $E$
    lies in
!

Remember

To find out the relative position, one tries to calculate the intersection.

  • clear intersection: $g$ and $E$ intersect
    (an intersection)

  • wrong statement (e.g. $0=5$): $g$ parallel to $E$
    (no intersection)

  • true statement (z. B. $5=5$): $g$ is in $E$
    (infinite intersections)
i

Hint

The easiest solution is with the plane's coordinate equation.
If the plane is in the parametric form, one would have to solve a system of linear equations with three equations and variables, which should be avoided due to the complexity.
i

Method

  1. Rewrite equation of a line
  2. Insert $x$, $y$, $z$ in the plane's cartesian equation and solve
  3. Interpret the result

Example

$\text{g: } \vec{x} = \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ -3 \\ 4 \end{pmatrix}$

$\text{E: } 2x+y+2z=-2$

  1. Rewrite equation of a line

    The vector $\vec{x}$ in the equation of a line is replaced by $\begin{pmatrix} x \\ y \\ z \end{pmatrix}$.

    $\begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ -3 \\ 4 \end{pmatrix}$

    Each line corresponds to an equation

    1. $x=\color{red}{2+2r}$
    2. $y=\color{blue}{1-3r}$
    3. $z=\color{green}{1+4r}$

  2. Insert $x$, $y$, $z$

    The individual equations for $x$, $y$, $z$ can be inserted into the plane's cartesian equation.

    $\text{E: } 2\color{red}{x}+\color{blue}{y}+2\color{green}{z}=-2$

    $2\cdot\color{red}{(2+2r)}$ $+\color{blue}{(1-3r)}$ $+2\cdot\color{green}{(1+4r)}$ $=-2$

    Now the brackets are solved and the equation is converted to $r$

    $4+4r+1-3r+2+8r$ $=-2$
    $7+9r=-2\quad|-7$
    $9r=-9\quad|:9$
    $r=-1$

  3. Interpret the result

    Since we have got a clear $r$, the plane and the straight line must intersect and you can calculate the intersection.

    => Line $g$ and plane $E$ intersect.

    The intersection is calculated by inserting $r=-1$ into the equation of a line.

    $\begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} + (-1) \cdot \begin{pmatrix} 2 \\ -3 \\ 4 \end{pmatrix}$ $=\begin{pmatrix} 0 \\ 4 \\ -3 \end{pmatrix}$

    => intersection $S(0|4|-3)$.