Relative position of spheres and planes
There are also three possible relationships for a sphere and a plane in three-dimensional space.
Remember
To determine the position, calculate the distance $d$ from the center of the sphere to the plane (see distance point plane).
The distance is now compared with the radius $r$.
$d>r$: no common points

$d=r$: common point of contact
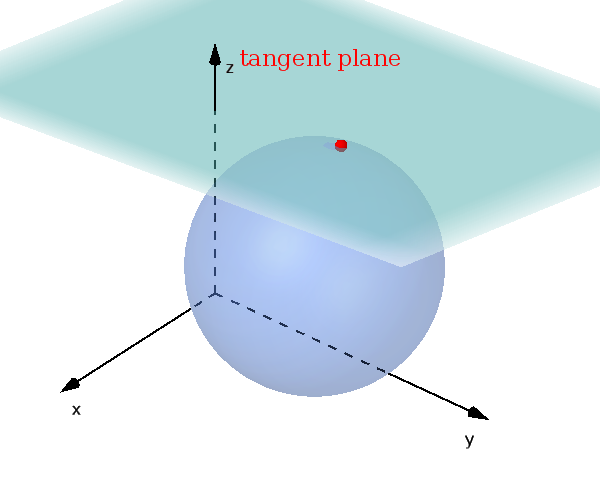
$d<r$: common circle of intersection
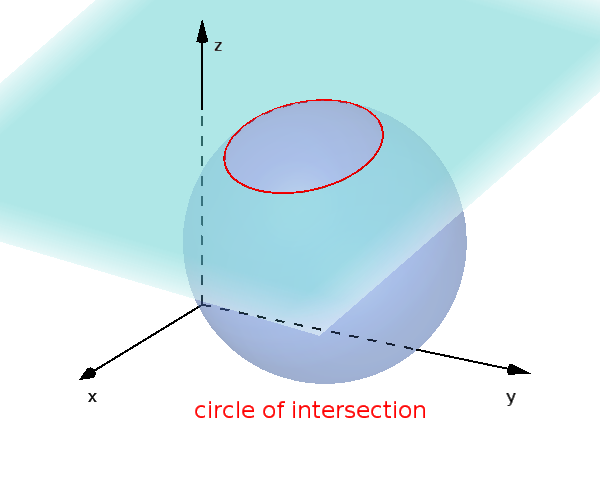
Info
Calculate circle of intersection
In the third case, the center $M'$ of the circle of intersection can be calculated. To do this, set up the following equation of a line.
$\vec{OM}$ is the center of the sphere and $\vec{n}$ is the normal vector of the plane.
The intersection of the line $g$ and plane $E$ is the center of the circle.
In addition, the radius $r'$ of this circle of intersection can also be determined.
Method
- Distance from $M$ to $E$
- Check $r$ and $d$ (3 conditions, see above)
- $M'$: Set up $g$ and intersection point with $E$
- Calculate radius $r'$
Example
$\text{E: } \left(\vec{x} - \begin{pmatrix} 5 \\4 \\ 3 \end{pmatrix}\right) \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}=0$
$k: (x+1)^2+(y-2)^2$ $+(z-1)^2=16$
-
Distance from $M$ to $E$
We can read off the center of the sphere from the sphere equation.
$M(-1|2|1)$
We calculate the distance from the center $M$ to the plane $E$. First we set up the Hesse normal form (HNF).
$|\vec{n}|=\left|\begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}\right|$ $=1$
Since the absolute value is 1, it is already a unit normal vector. We already have the HNF.
$\left(\vec{x} - \begin{pmatrix} 5 \\4 \\ 3 \end{pmatrix}\right) \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}=0$
The center point now only needs to be inserted for the distance calculation.
$d=\left|\left(\begin{pmatrix} -1 \\ 2 \\ 1 \end{pmatrix} - \begin{pmatrix} 5 \\4 \\ 3 \end{pmatrix}\right) \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}\right|$
$d=\left|\begin{pmatrix} -6 \\ 8 \\ -2 \end{pmatrix} \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}\right|$
$d=\left|0+0-2\right|$ $=|-2|$ $=2$
-
Check condition
First you read the radius from the sphere equation.
$r=\sqrt{16}=4$
We now look at which of the three cases is present.
$2<4$
$d<r$
The distance is smaller than the radius ($d<r$), the plane lies in the sphere and there is therefore a circle of intersection.
-
Set up line $g$ and intersection point with $E$
Now it's about calculating the new center of the circle of intersection. A equation of a line is set up as described above.
$g: \vec{x} = \vec{OM} + t \cdot \vec{n}$
$g: \vec{x} = \begin{pmatrix} -1 \\ 2 \\ 1 \end{pmatrix} + t \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}$
The intersection of the line and the plane corresponds to the center $M'$.
The equation of a line is inserted for $\vec{x}$ in the plane.
$(\begin{pmatrix} -1 \\ 2 \\ 1 \end{pmatrix}$ $+ t \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}$ $- \begin{pmatrix} 5 \\4 \\ 3 \end{pmatrix}) \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}=0$
$\begin{pmatrix} -6 \\ -2 \\ t-2 \end{pmatrix} \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}=0$
$0+0+1\cdot(t-2)=0$
$t-2=0\quad|+2$
$t=2$The center $M'$ is obtained by inserting the calculated $t$ into the equation of a line.
$\vec{OM'} = \begin{pmatrix} -1 \\ 2 \\ 1 \end{pmatrix} + 2 \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}$ $=\begin{pmatrix} -1 \\ 2 \\ 3 \end{pmatrix}$
$M'(-1|2|3)$
-
Calculate radius $r'$
Finally calculate the radius of the circle of intersection.
To do this, insert the previously calculated $d$ and the read radius $r$ of the sphere into the following formula:
$r'=\sqrt{r^2-d^2}$
$r'=\sqrt{4^2-2^2}$ $=\sqrt{12}$ $\approx3.46$
The circle of intersection has the center $M'(-1|2|3)$ and the radius $r\approx3.46$
