Circle through 3 points

A circle is clearly defined by 3 points that are not on a line.

To calculate, think of a triangle from the 3 points. The intersection of the triangle's perpendicular bisector is the centre.

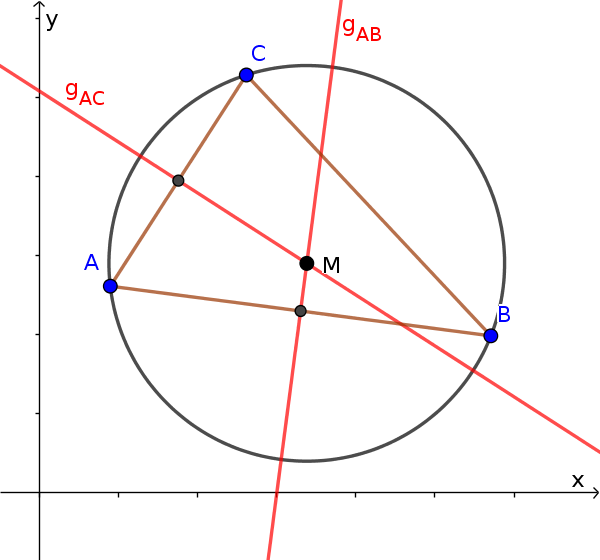
It is therefore sufficient to set up the equation of a line of two perpendicular bisectors and to calculate the intersection point.

Example

$A(5|2)$, $B(1|2)$, $C(1|4)$

1. Centre on two sides

   We choose two sides of the triangle, e.g. AB and AC. We now want to set up two equations of a line of the perpendicular bisector. The centre of the corresponding side serves as the support point.

   Support point for $g_{AB}$

   We calculate the centre of the two points $A$ and $B$.

   $M_{AB}(\frac{5+1}{2}|\frac{2+2}{2})$
   $M_{AB}(3|2)$

   
   

   Support point for $g_{AC}$

   We calculate the centre of the two points $A$ and $C$.

   $M_{AB}(\frac{5+1}{2}|\frac{2+4}{2})$
   $M_{AB}(3|3)$

2. Normal vector on two sides

   A vertical vector is now determined for each of the two sides selected. This serves as the direction vector for the line, so that it lies vertically on the side (prerequisite for a perpendicular bisector).

   Direction vector for $g_{AB}$

   A vector must be found with which the scalar product results in zero (= vectors perpendicular).

   $\vec{AB}\cdot\vec{n_{AB}}=0$

   $\begin{pmatrix} -4 \\ 0 \end{pmatrix}\cdot\color{blue}{\begin{pmatrix} \, \\ \, \end{pmatrix}} = 0$

   It is particularly easy if you swap the two coordinates and change exactly one sign.

   $\begin{pmatrix} \color{red}{-4} \\ \color{red}{0} \end{pmatrix}\cdot\begin{pmatrix} \color{blue}{0} \\ \color{blue}{+4} \end{pmatrix} = 0$

   $\vec{n_{AB}}=\begin{pmatrix} 0 \\ 4 \end{pmatrix}$

   
   

   Direction vector for $g_{AC}$

   $\vec{AC}\cdot\vec{n_{AC}}=0$

   $\begin{pmatrix} -4 \\ 2 \end{pmatrix}\cdot\color{blue}{\begin{pmatrix} \, \\ \, \end{pmatrix}} = 0$

   $\begin{pmatrix} \color{red}{-4} \\ \color{red}{2} \end{pmatrix}\cdot\begin{pmatrix} \color{blue}{2} \\ \color{blue}{+4} \end{pmatrix} = 0$

   $\vec{n_{AC}}=\begin{pmatrix} 2 \\ 4 \end{pmatrix}$

3. Equation of a line

   Set up equation of a line with the support vector and the direction vector.

   Equation of a line for $g_{AB}$

   $g_{AB}: \vec{x} = \vec{OM_{AB}} + r \cdot \vec{n_{AB}}$

   $g_{AB}: \vec{x} = \begin{pmatrix} 3 \\ 2 \end{pmatrix} + r \cdot \begin{pmatrix} 0 \\ 4 \end{pmatrix}$

   
   

   Equation of a line for $g_{AC}$

   $g_{AC}: \vec{x} = \vec{OM_{AC}} + s \cdot \vec{n_{AC}}$

   $g_{AC}: \vec{x} = \begin{pmatrix} 3 \\ 3 \end{pmatrix} + s \cdot \begin{pmatrix} 2 \\ 4 \end{pmatrix}$

4. Determine the centre of the circle

   The centre is the intersection point of the line.

   $g_{AB}: \vec{x} = \begin{pmatrix} 3 \\ 2 \end{pmatrix} + r \cdot \begin{pmatrix} 0 \\ 4 \end{pmatrix}$

   $g_{AC}: \vec{x} = \begin{pmatrix} 3 \\ 3 \end{pmatrix} + s\cdot \begin{pmatrix} 2 \\ 4 \end{pmatrix}$

   
   

   $\begin{pmatrix} 3 \\ 2 \end{pmatrix} + r \cdot \begin{pmatrix} 0 \\ 4 \end{pmatrix}$ $=\begin{pmatrix} 3 \\ 3 \end{pmatrix} + s\cdot \begin{pmatrix} 2 \\ 4 \end{pmatrix}$

   Set up a system of equations

   1. $3=3+2s$
   2. $2+4r=3+4s$

   Solve system of equations

   $3=3+2s\quad|-3$
   $2s=0\quad|:2$
   $s=0$

   $2+4r=3+4\cdot0\quad|-2$
   $4r=1\quad|:4$
   $r=\frac14$

   
   

   Insert $s$ or $r$ in the corresponding equation of a line to get the intersection point or centre of the circle.

   $\vec{OM} = \begin{pmatrix} 3 \\ 3 \end{pmatrix} + 0\cdot \begin{pmatrix} 2 \\ 4 \end{pmatrix}$ $=\begin{pmatrix} 3 \\ 3 \end{pmatrix}$

   The centre is at $M(3|3)$

5. Determine the radius of the circle

   First we set up the equation of a circle with the centre.

   $(x-x_M)^2+(y-y_M)^2=r^2$

   $(x-3)^2+(y-3)^2=r^2$

   The radius can be determined by inserting a point on the circle into the equation of a circle.

   $A(5|2)$

   $(5-3)^2+(2-3)^2=r^2$
   $2^2+(-1)^2=r^2$
   $5=r^2\quad|\sqrt{}$
   $r=\sqrt{5}$

   The equation of a circle is:

   $(x-3)^2+(y-3)^2=5$

   The circle has the centre $M(3|3)$ and the radius $r=\sqrt{5}$