Tangent plane

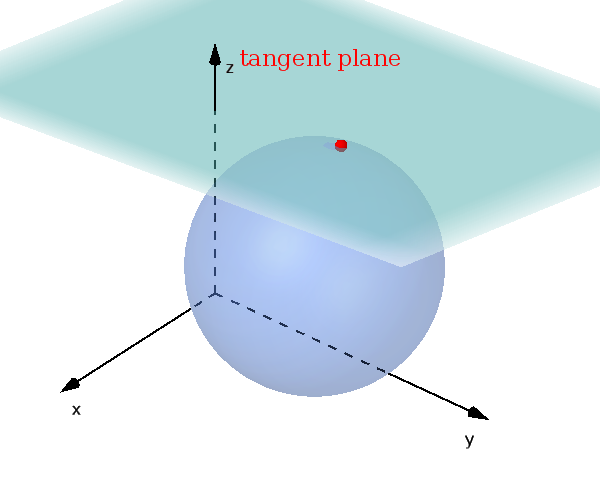
A relative position between sphere and plane is the tangent plane.

Set up the tangent plane

If you have given the center $M$ of a sphere and the point of contact $B$, you can use the following formula to set up a tangent plane.

Calculate point of contact

In the case of a tangent plane, the distance $d$ from the center of the sphere to the plane corresponds to the radius $r$ (see distance plane and point).

The point of contact $B$ can be calculated. To do this, set up the following equation of a line:

$\vec{OM}$ is the center of the sphere and $\vec{n}$ is the normal vector of the plane.

The intersection of the line $g$ and plane $E$ is the point of contact.

Example

$\text{E: } \left(\vec{x} - \begin{pmatrix} 5 \\4 \\ 3 \end{pmatrix}\right) \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}=0$

$k: (x+1)^2+(y-2)^2$ $+(z-1)^2=4$

1. Distance from $M$ to $E$

   We can read the center of the sphere from the sphere equation.

   $M(-1|2|1)$

   We calculate the distance from the center $M$ to the plane $E$. First we set up the Hesse normal form.

   $|\vec{n}|=\left|\begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}\right|$ $=1$

   Since the absolute value is 1, it is already a unit normal vector. We already have the Hesse normal form.

   $\left(\vec{x} - \begin{pmatrix} 5 \\4 \\ 3 \end{pmatrix}\right) \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}=0$

   The center point now only needs to be inserted for the distance calculation.

   $d=\left|\left(\begin{pmatrix} -1 \\ 2 \\ 1 \end{pmatrix} - \begin{pmatrix} 5 \\4 \\ 3 \end{pmatrix}\right) \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}\right|$

   $d=\left|\begin{pmatrix} -6 \\ 8 \\ -2 \end{pmatrix} \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}\right|$

   $d=\left|0+0-2\right|$ $=|-2|$ $=2$

2. Check condition

   First you read the radius from the sphere equation.

   $r=\sqrt{4}=2$

   We now look at which of the three cases is present.

   $2=2$

   $d=r$

   The distance is equal to the radius ($d=r$), the plane touches the sphere and there is therefore a point of contact.

3. Set up $g$ and intersection point with $E$

   Now it's about calculating the new point of contact. An equation of a line is set up as described above.

   $g: \vec{x} = \vec{OM} + t \cdot \vec{n}$

   $g: \vec{x} = \begin{pmatrix} -1 \\ 2 \\ 1 \end{pmatrix} + t \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}$

   The intersection point of the line and the plane corresponds to the point of contact $B$.

   The straight line equation is inserted for $\vec{x}$ in the plane.

   $(\begin{pmatrix} -1 \\ 2 \\ 1 \end{pmatrix}$ $+ t \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}$ $- \begin{pmatrix} 5 \\4 \\ 3 \end{pmatrix}) \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}=0$

   
   

   $\begin{pmatrix} -6 \\ -2 \\ t-2 \end{pmatrix} \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}=0$

   $0+0+1\cdot(t-2)=0$
   $t-2=0\quad|+2$
   $t=2$

   The point of contact $B$ is obtained by inserting the calculated $t$ into the equation of a line.

   $\vec{OB} = \begin{pmatrix} -1 \\ 2 \\ 1 \end{pmatrix} + 2 \cdot \begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}$ $=\begin{pmatrix} -1 \\ 2 \\ 3 \end{pmatrix}$

   $B(-1|2|3)$