Math ↠ Circles and spheres ↠ Spheres in three-dimensional space

Spheres in three-dimensional space (3D)

Similar to the circles in the plane there are spheres in three-dimensional space.

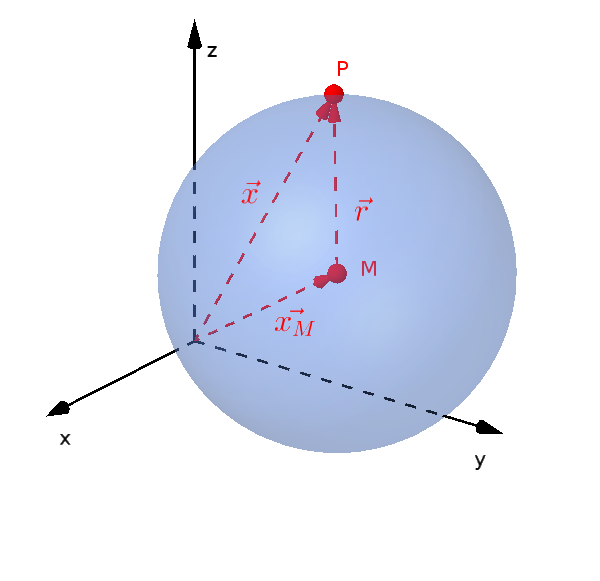
A vector representation is also possible for spheres.

$(\vec{x}-\vec{x_M})^2=r^2$

Like the circles, the cartesian equation of the sphere is derived from this.

$(x-x_M)^2+(y-y_M)^2$ $+(z-z_M)^2=r^2$

  • $r$ is the radius
  • $M(x_M|y_M|z_M)$ is the center
i

Hint

Spheres in 3D have many similarities to the circles in the plane (2D). Since we are in space, there is also a z coordinate for the spheres.

Point on sphere: position of point and sphere

We also insert the point $P(x_0|y_0|z_0)$ in the front part of the sphere equation.

$(x_0-x_M)^2+(y_0-y_M)^2$ $+(z-z_M)^2$

Now we distinguish 3 cases again. The result is

  • $=r^2$: The point is on the sphere.
  • $<r^2$: The point is inside the sphere.
  • $>r^2$: The point is outside the sphere.