Kugeln im Raum (3D)
Analog zu den Kreisen in der Ebene gibt es Kugeln im Raum.
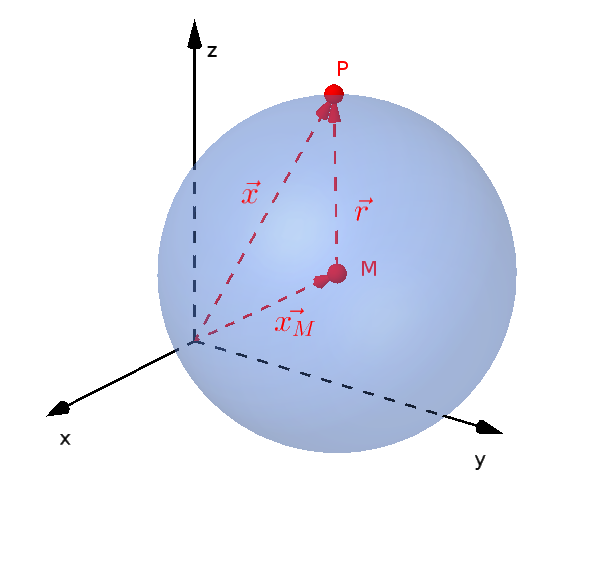
Bei Kugeln ist ebenso eine vektorielle Darstellung möglich.
$(\vec{x}-\vec{x_M})^2=r^2$
Daraus leitet sich wie bei den Kreisen die Koordinatengleichung der Kugel her.
$(x-x_M)^2+(y-y_M)^2$ $+(z-z_M)^2=r^2$
- $r$ ist der Radius
- $M(x_M|y_M|z_M)$ ist der Mittelpunkt
i
Tipp
Kugeln in 3D haben viele Ähnlichkeiten zu den Kreisen in der Ebene (2D). Da wir uns im Raum befinden, kommt bei den Kugeln jedoch noch eine $z$-Koordinate hinzu.
Punktprobe: Lage von Punkt und Kugel
Wir setzen auch hier den Punkt $P(x_0|y_0|z_0)$ in den vorderen Teil der Kugelgleichung ein.
$(x_0-x_M)^2+(y_0-y_M)^2$ $+(z-z_M)^2$
Nun unterscheiden wir wieder 3 Fälle. Das Ergebnis ist
- $=r^2$: Der Punkt liegt auf der Kugel.
- $<r^2$: Der Punkt liegt innerhalb der Kugel.
- $>r^2$: Der Punkt liegt außerhalb der Kugel.
