Mathe ↠ Kreise und Kugeln ↠ Lage Kreis und Punkt

Lage eines Punktes zu einem Kreis

Mit der Kreisgleichung lässt sich überprüfen, wo ein Punkt relativ zum Kreis liegt.

!

Merke

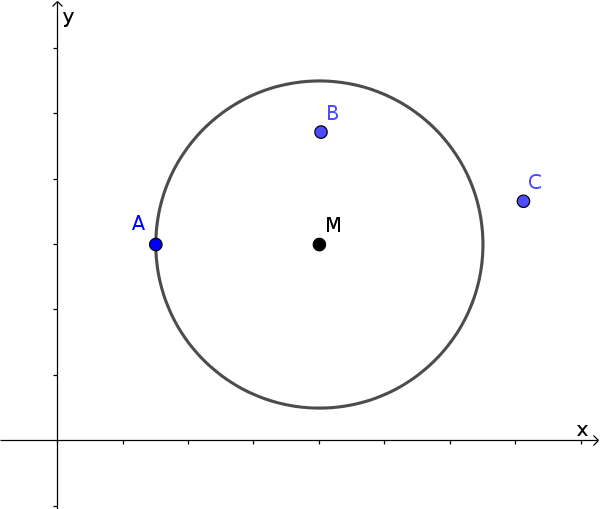
Ein Punkt kann auf, innerhalb und außerhalb eines Kreises liegen.

Der Abstand des Punktes zum Mittelpunkt ist dann gleich, kleiner oder größer als der Radius.

Zur Bestimmung der Lage von $P(x_0|y_0)$ zum Mittelpunkt $M(x_M|y_M)$ wird dieser in den vorderen Teil der Koordinatengleichung eingesetzt.

$(x_0-x_M)^2+(y_0-y_M)^2$

Nun unterscheiden wir 3 Fälle. Das Ergebnis ist

  • $=r^2$: Der Punkt liegt auf dem Kreis.
  • $<r^2$: Der Punkt liegt im Kreis.
  • $>r^2$: Der Punkt liegt außerhalb des Kreises.

Etwas einfacher kann man auch mit dem Betrag des Vektors $\vec{MP}$ rechnen. (Achtung hier wird dann auf $r$, nicht $r^2$ überprüft!)

  • $|\vec{MP}|=r$: Der Punkt liegt auf dem Kreis.
  • $|\vec{MP}|<r$: Der Punkt liegt im Kreis.
  • $|\vec{MP}|>r$: Der Punkt liegt außerhalb des Kreises.

Beispiel

Bestimme die Lage des Punktes $P(3|3)$ zum Kreis $k$.

$k: (x-2)^2+(y+1)^2=25$

  1. Punkt einsetzen

    $(3-2)^2+(3+1)^2$ $=1^2+4^2$ $=17$

  2. Überprüfen

    $17 \, ? \, r^2$

    $17 < 25$

    Der Punkt $P$ liegt innerhalb des Kreises.