Kreis durch 3 Punkte

Ein Kreis ist durch 3 Punkte, die nicht auf einer Geraden liegen, eindeutig festgelegt.

Zum Berechnen denkt man sich ein Dreieck aus den 3 Punkten. Der Schnittpunkt der Mittelsenkrechten des Dreiecks ist der Mittelpunkt.

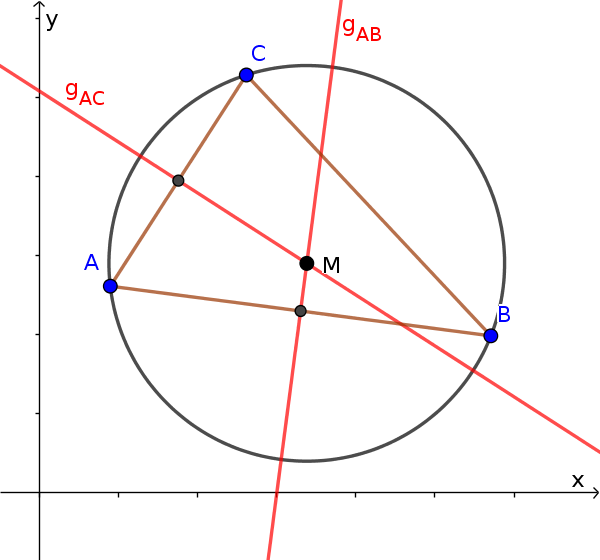
Es reicht also die Geradengleichungen von zwei Mittelsenkrechten aufzustellen und den Schnittpunkt zu berechnen.

Beispiel

$A(5|2)$, $B(1|2)$, $C(1|4)$

1. Mittelpunkte bei zwei Seiten

   Wir suchen uns zwei Seiten des Dreiecks aus, z. B. AB und AC. Wir wollen nun zwei Geradengleichungen der Mittelsenkrechten aufstellen. Als Stützpunkt dient jeweils der Mittelpunkt der zugehörigen Seite.

   Stützpunkt für $g_{AB}$

   Wir berechnen den Mittelpunkt der beiden Punkte $A$ und $B$.

   $M_{AB}(\frac{5+1}{2}|\frac{2+2}{2})$
   $M_{AB}(3|2)$

   
   

   Stützpunkt für $g_{AC}$

   Wir berechnen den Mittelpunkt der beiden Punkte $A$ und $C$.

   $M_{AB}(\frac{5+1}{2}|\frac{2+4}{2})$
   $M_{AB}(3|3)$

2. Normalenvektor bei zwei Seiten

   Für die beiden gewählten Seiten wird nun jeweils ein senkrechter Vektor bestimmt. Dieser dient für die Gerade als Richtungsvektor, sodass sie senkrecht auf der Seite liegt (Voraussetzung für eine Mittelsenkrechte).

   Richungsvektor für $g_{AB}$

   Es muss ein Vektor gefunden werden, mit dem das Skalarprodukt null ergibt (= Vektoren senkrecht).

   $\vec{AB}\cdot\vec{n_{AB}}=0$

   $\begin{pmatrix} -4 \\ 0 \end{pmatrix}\cdot\color{blue}{\begin{pmatrix} \, \\ \, \end{pmatrix}} = 0$

   Besonders einfach ist es, wenn man die beiden Koordinaten tauscht und genau ein Vorzeichen verändert.

   $\begin{pmatrix} \color{red}{-4} \\ \color{red}{0} \end{pmatrix}\cdot\begin{pmatrix} \color{blue}{0} \\ \color{blue}{+4} \end{pmatrix} = 0$

   $\vec{n_{AB}}=\begin{pmatrix} 0 \\ 4 \end{pmatrix}$

   
   

   Richtungsvektor für $g_{AC}$

   $\vec{AC}\cdot\vec{n_{AC}}=0$

   $\begin{pmatrix} -4 \\ 2 \end{pmatrix}\cdot\color{blue}{\begin{pmatrix} \, \\ \, \end{pmatrix}} = 0$

   $\begin{pmatrix} \color{red}{-4} \\ \color{red}{2} \end{pmatrix}\cdot\begin{pmatrix} \color{blue}{2} \\ \color{blue}{+4} \end{pmatrix} = 0$

   $\vec{n_{AC}}=\begin{pmatrix} 2 \\ 4 \end{pmatrix}$

3. Geradengleichungen

   Mit dem Stützvektor und dem Richtungsvektor Geradengleichungen aufstellen.

   Geradengleichung für $g_{AB}$

   $g_{AB}: \vec{x} = \vec{OM_{AB}} + r \cdot \vec{n_{AB}}$

   $g_{AB}: \vec{x} = \begin{pmatrix} 3 \\ 2 \end{pmatrix} + r \cdot \begin{pmatrix} 0 \\ 4 \end{pmatrix}$

   
   

   Geradengleichung für $g_{AC}$

   $g_{AC}: \vec{x} = \vec{OM_{AC}} + s \cdot \vec{n_{AC}}$

   $g_{AC}: \vec{x} = \begin{pmatrix} 3 \\ 3 \end{pmatrix} + s \cdot \begin{pmatrix} 2 \\ 4 \end{pmatrix}$

4. Mittelpunkt des Kreises bestimmen

   Der Mittelpunkt ist der Schnittpunkt der Geraden.

   $g_{AB}: \vec{x} = \begin{pmatrix} 3 \\ 2 \end{pmatrix} + r \cdot \begin{pmatrix} 0 \\ 4 \end{pmatrix}$

   $g_{AC}: \vec{x} = \begin{pmatrix} 3 \\ 3 \end{pmatrix} + s\cdot \begin{pmatrix} 2 \\ 4 \end{pmatrix}$

   
   

   $\begin{pmatrix} 3 \\ 2 \end{pmatrix} + r \cdot \begin{pmatrix} 0 \\ 4 \end{pmatrix}$ $=\begin{pmatrix} 3 \\ 3 \end{pmatrix} + s\cdot \begin{pmatrix} 2 \\ 4 \end{pmatrix}$

   Gleichungssystem aufstellen

   1. $3=3+2s$
   2. $2+4r=3+4s$

   Gleichungssystem lösen

   $3=3+2s\quad|-3$
   $2s=0\quad|:2$
   $s=0$

   $2+4r=3+4\cdot0\quad|-2$
   $4r=1\quad|:4$
   $r=\frac14$

   
   

   $s$ oder $r$ in die zugehörige Geradengleichung einsetzen, um Schnittpunkt bzw. Mittelpunkt des Kreises zu erhalten.

   $\vec{OM} = \begin{pmatrix} 3 \\ 3 \end{pmatrix} + 0\cdot \begin{pmatrix} 2 \\ 4 \end{pmatrix}$ $=\begin{pmatrix} 3 \\ 3 \end{pmatrix}$

   Der Mittelpunkt ist bei $M(3|3)$

5. Radius des Kreises bestimmen

   Zuerst stellen wir die Kreisgleichung mit dem Mittelpunkt auf.

   $(x-x_M)^2+(y-y_M)^2=r^2$

   $(x-3)^2+(y-3)^2=r^2$

   Der Radius kann ermittelt werden, indem ein Punkt auf dem Kreis in die Kreisgleichung eingesetzt wird.

   $A(5|2)$

   $(5-3)^2+(2-3)^2=r^2$
   $2^2+(-1)^2=r^2$
   $5=r^2\quad|\sqrt{}$
   $r=\sqrt{5}$

   Die Kreisgleichung lautet:

   $(x-3)^2+(y-3)^2=5$

   Der Kreis hat den Mittelpunkt $M(3|3)$ und den Radius $r=\sqrt{5}$