Math ↠ Circles and spheres ↠ Position circle and point

Position of a point relative to a circle

The equation of a circle can be used to check where a point lies relative to the circle.

!

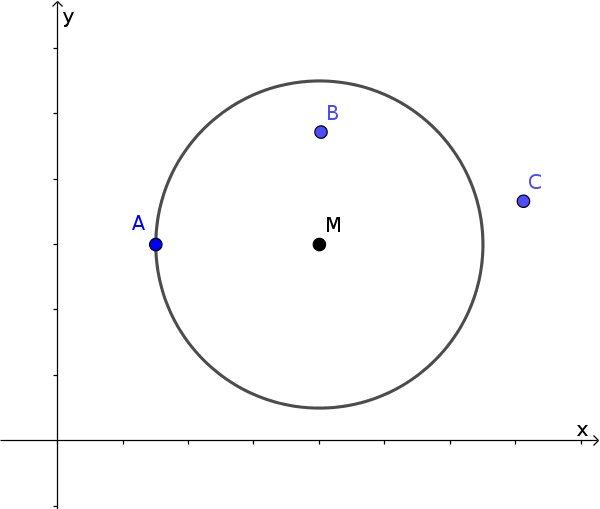
Remember

A point can lie on, inside and outside a circle.

The distance from the point to the centre is then the same, smaller or larger than the radius.

To determine the position of $P(x_0|y_0)$ from the centre $M(x_M|y_M)$, this point is inserted in the front part of the cartesian equation.

$(x_0-x_M)^2+(y_0-y_M)^2$

We now distinguish 3 cases. The result is

  • $=r^2$: The point is on the circle.
  • $<r^2$: The point is in the circle.
  • $>r^2$: The point is outside the circle.

It is also easier to calculate with the magnitude of the vector $\vec{MP}$. (Attention, then it is checked for $r$, not $r^2$!)

  • $|\vec{MP}|=r$: The point is on the circle.
  • $|\vec{MP}|<r$: The point is in the circle.
  • $|\vec{MP}|>r$: The point is outside the circle.

Example

Find the position of point $P(3|3)$ to circle $k$.

$k: (x-2)^2+(y+1)^2=25$

  1. Insert point

    $(3-2)^2+(3+1)^2$ $=1^2+4^2$ $=17$

  2. Check

    $17 \, ? \, r^2$

    $17 < 25$

    The point $P$ lies within the circle.