Differenzenquotient
Im Gegensatz zu linearen Funktionen besitzen andere Funktionstypen keine konstante Steigung.
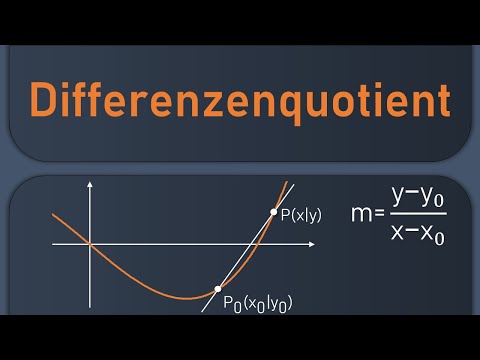
Zur Berechnung der durchschnittlichen Steigung zwischen zwei Punkten $P_1(x_0|f(x_0))$ und $P_2(x|f(x))$ nutzt man daher den Differenzenquotienten:
Merke
Der Differenzenquotient ist die Steigung der Sekanten, die durch die Punkte $P_1(x_0|f(x_0))$ und $P_2(x|f(x))$ geht.
Tipp

Beispiel
Bestimme den Differenzenquotient der Funktion $f(x)=x^2$ von den beiden Punkten $P_1(2|f(2))$ und $P_2(5|f(5))$
$m=\frac{f(x)-f(x_0)}{x-x_0}=\frac{f(5)-f(2)}{5-2}$ $=\frac{5^2-2^2}{3}$ $=\frac{25-4}{3}$ $=\frac{21}{3}=7$Differenzenquotient, Ableitung, Steigung zwischen zwei Punkten
Viele Funktionsgraphen sind keine Geraden sondern Kurven und haben somit keine einheitliche Steigung. Häufig interessiert einen trotzdem, welche Steigung zwischen zwei Punkten auf einem Graphen durchschnittlich vorliegt.
Dazu stellt man eine Gerade auf, die durch die beiden Punkte verläuft. Eine solche Gerade, die durch (mindestens) zwei Punkte einer Kurve verläuft, bezeichnet man als Sekante. Es handelt sich nun um die Steigungsberechnung einer linearen Funktion.