Ableitung und Differenzierbarkeit
Als Differenzialrechnung (oder Differentialrechnung) bezeichnet man ein Teilgebiet der Analysis, das sich mit dem Studium von Funktionen mithilfe der Ableitung beschäftigt.
Mit der Ableitung wird dabei die Steigung an einem Punkt des Funktionsgraphen bestimmt.
Differenzenquotient
Bereits bekannt ist, wie man die Steigung einer linearen Funktion bestimmt. Dies wird beim Differenzenquotienten ausgenutzt, um die mittlere Steigung zwischen zwei Punkten $P_1(x_0|f(x_0))$ und $P_2(x|f(x))$ zu bestimmen.
Eine lineare Funktion kann mit zwei gegebenen Punkten genau definiert werden. Entsprechend stellt man eine Gerade, die sogenannte Sekante, auf, welche die beiden gewählten Punkte schneidet. Ihre Steigung entspricht der durchschnittlichen Änderungsrate (Steigung) zwischen den beiden Punkten.

Differenzialquotient
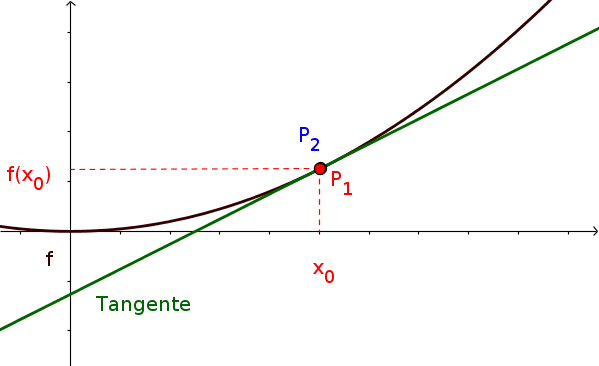
Nun interessiert einen in der Differenzialrechnung nicht nur die Steigung zwischen zwei Punkten, sondern die Änderungsrate an genau einem Punkt einer Funktion. Man wählt dazu den zweiten Punkt mit unendlich kleinem Abstand zum Ausgangspunkt, sodass man schließlich eine Gerade erhält, die genau am ursprünglichen Punkt anliegt. Diese Gerade nennt sich Tangente und ihre Steigung entspricht dem Differenzialquotienten.
Mathematisch ausgedrückt wird der unendlich kleine Abstand mit Hilfe des limes. Der Differenzialquotient ist somit der Grenzwert des Differenzenquotienten:
Differenzierbarkeit
Eine Funktion ist differenzierbar, wenn jede Stelle der Funktion differenzierbar ist. Bei einer differenzierbaren Funktion darf es keine nicht differenzierbare Stelle geben.
Ableitung
Die Ableitungsfunktion (kurz Ableitung) ordnet jedem $x$ den entsprechenden Differenzialquotienten zu. Dadurch muss nicht ständig der Differenzialquotient neu berechnet werden, sondern kann die gesuchte Stelle einfach in die Ableitungsfunktion einsetzen, um die Steigung zu bestimmen. Das Berechnen der Ableitung $f'$ einer Funktion $f$ nennt man Ableiten oder Differenzieren.
Ableitungsregeln
Die wichtigsten Ableitungsregeln sollte man beherrschen und vereinfachen einem das Berechnen der Ableitung enorm.
| Funktion | Ableitung | |
|---|---|---|
| Konstanten-, Potenz- und Faktorregel | ||
| $f(x)=c$ | $f'(x)=0$ | |
| $f(x)=x^n$ | $f'(x)=n\cdot x^{n-1}$ | |
| $f(x)=k\cdot g(x)$ | $f'(x)=k\cdot g'(x)$ | |
| Summenregel | ||
| $f(x)=g(x)+h(x)$ | $f'(x)=g'(x)+h'(x)$ | |
| Produktregel | ||
| $f(x)=g(x)\cdot h(x)$ | $f'(x)=g'(x)\cdot h(x)$ $+h'(x)\cdot g(x)$ | |
| Quotientenregel | ||
| $f(x)=\frac{g(x)}{h(x)}$ | $f'(x)=\frac{g'(x)\cdot h(x) -h'(x)\cdot g(x)}{(h(x))^2}$ | |
| Kettenregel | ||
| $f(x)=g(h(x))$ | $f'(x)=g'(h(x))\cdot h'(x)$ | |
Wichtige Funktionen
Auch die Ableitungen einiger elementarer Funktionen sollte man auswendig kennen
| Funktion | Ableitung | |
|---|---|---|
| Ableitung Potenz- und Wurzelfunktionen | ||
| $f(x)=x^n$ | $f'(x)=n\cdot x^{n-1}$ | |
| $f(x)=\sqrt{x}$ | $f'(x)=\frac{1}{2\sqrt{x}}$ | |
| Ableitung trigonometrische Funktionen | ||
| $f(x)=\sin(x)$ | $f'(x)=\cos(x)$ | |
| $f(x)=\cos(x)$ | $f'(x)=-\sin(x)$ | |
| $f(x)=\tan(x)$ | $f'(x)=\frac{1}{\cos^2(x)}$ | |
| Ableitung Exponentialfunktionen | ||
| $f(x)=a^x$ | $f'(x)=a^x\cdot\ln(a)$ | |
| $f(x)=e^x$ | $f'(x)=e^x$ | |
| Ableitung Logarithmusfunktionen | ||
| $f(x)=\log_a(x)$ | $f'(x)=\frac{1}{x\cdot\ln(a)}$ | |
| $f(x)=\ln(x)$ | $f'(x)=\frac{1}{x}$ | |
Lernen
Üben Premium
-
Grundlagen
2 Aufgaben -
Differenzen- und Differenzialquotient
3 Aufgaben -
Ableiten elementarer Funktionen
3 Aufgaben

