Difference Quotient
In contrast to linear functions,other function types do not have a constant slope.
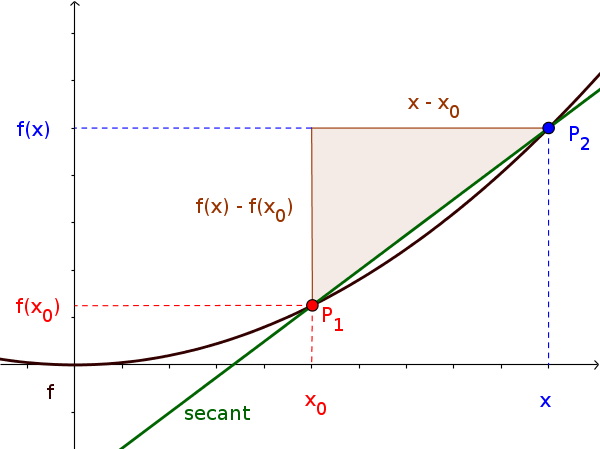
To calculate the average slope between two points $P_1(x_0|f(x_0))$ and $P_2(x|f(x))$ one uses the difference quotient:
$\frac{f(x)-f(x_0)}{x-x_0}$
!
Remember
The difference quotient is the average slope between two points.
The difference quotient is the slope of the secant, going through points $P_1(x_0|f(x_0))$ and $P_2(x|f(x))$.
i
Tip
Basically, one just draws a line (the secant) through the points and calculates it like the slope of a linear function:
$m=\frac{\Delta y}{\Delta x}=\frac{f(x)-f(x_0)}{x-x_0}$
Example
Determine the difference quotient of the function $f(x)=x^2$ of the points $P_1(2|f(2))$ and $P_2(5|f(5))$
$m=\frac{f(x)-f(x_0)}{x-x_0}=\frac{f(5)-f(2)}{5-2}$ $=\frac{5^2-2^2}{3}$ $=\frac{25-4}{3}$ $=\frac{21}{3}=7$