Differential Quotient
The differential quotient is the limit of the difference quotient:
$\lim\limits_{x \to x_0}{\frac{f(x)-f(x_0)}{x - x_0}}$
!
Remember
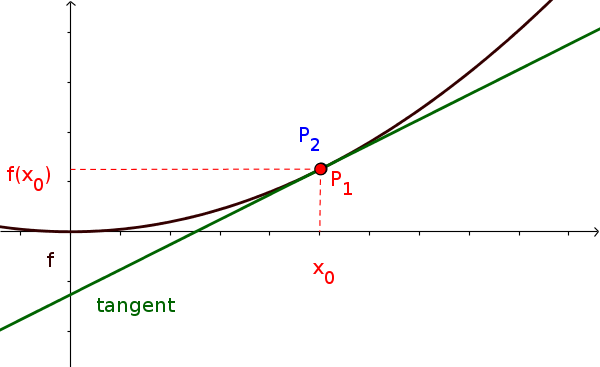
The differential quotient (also called derivative) corresponds to the slope at a specific point of a function.
Geometrically, the differential quotient corresponds to the slope of the tangent of a point.
Considering the secant, let the distance of the points be infinitely small until you get a tangent.
Example
Determine the slope of the function $f(x)=x^2$ at the point $x_0=1$ using the differential quotient.
-
Inserting
$\lim\limits_{x \to x_0}{\frac{f(x)-f(x_0)}{x - x_0}}$
For $x_0$ insert $1$ and for $f(x)$ insert $x^2$
$\lim\limits_{x \to 1}{\frac{x^2-f(1)}{x - 1}}$ $=\lim\limits_{x \to 1}{\frac{x^2-1^2}{x - 1}}$ $=\lim\limits_{x \to 1}{\frac{x^2-1}{x - 1}}$ -
Simplifying fraction
The fraction has to be simplified as, inserting 1 for $x$, the denominator becomes $0$ (division by 0 forbidden!).
$\lim\limits_{x \to 1}{\frac{x^2-1}{x - 1}}$
In this case it's easiest to reshape and reduce the fraction. If that doesn't work, one has to use polinomial division.
$\lim\limits_{x \to 1}{\frac{(x-1)(x+1)}{(x-1)}}=\lim\limits_{x \to 1}{(x+1)}$ -
Inserting $x_0=1$ for $x$
Letting $x$ go towards 0, one gets the slope.
$\lim\limits_{x \to 1}{(\overbrace{x}^{\to 1}+1)}=1+1=2$
i
Tip
To prevent the complicated calculation with the limit and the differential quotient, there are the derivative functions.
