Polstelle

Eine Definitionslücke heißt Polstelle einer gebrochenrationalen Funktion, wenn die Funktionswerte bei Annäherung an die Stelle beliebig groß (klein) werden.

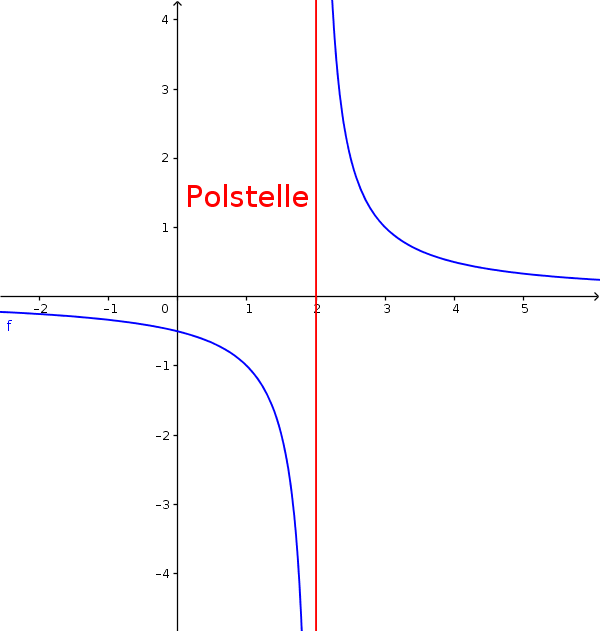
Die Voraussetzung für eine Polstelle ist, dass das Nennerpolynom den Wert Null und das Zählerpolynom einen Wert ungleich Null annimmt.

!

Merke

Eine gebrochenrationale Funktion
$f(x)=\frac{g(x)}{h(x)}$
besitzt eine Polstelle, wenn gilt:
$g(x)\neq0$ und $h(x)=0$
!

Beachte

Eine Definitionslücke kann auch, wenn die Bedingung nicht erfüllt ist, eine Polstelle sein. Um diesen Sonderfall zu überprüfen, kürzt man die Funktion vollständig. Falls die Nullstelle noch Definitionslücke des gekürzten Funktionsterms ist, handelt es sich um eine Polstelle.

Häufig wird in der Schule dieser Sonderfall jedoch nicht betrachtet. Dann kann Schritt IV. (ggf. auch III.) weggelassen werden.

i

Vorgehensweise

  1. Nullstelle des Nenners berechnen (Definitionslücke bestimmen)
  2. Nullstelle(n) des Nenners in Zähler einsetzen
  3. Bedingung überprüfen

    4. Wenn Bedinung nicht stimmt:
  4. Kürzen: Prüfen, ob Polstelle oder hebbare Definitionslücke

Beispiel

Aufgabe: Berechne die Polstelle der Funktion

$f(x)=\frac{3x-6}{x^2+x-6}$

  1. Nullstelle des Nenners berechnen

    $x^2+x-6=0$
    In dem Fall liegt eine quadratische Gleichung vor, die man beispielsweise mit der PQ-Formel lösen kann.
    $x_{1,2} = -\frac{p}{2} \pm\sqrt{(\frac{p}{2})^2-q}$
    $x_{1,2} = -\frac{1}{2} \pm\sqrt{(\frac{1}{2})^2+6}$
    $x_{1,2} = -\frac{1}{2} \pm\sqrt{\frac{25}{4}}$
    $x_{1,2} = -\frac{1}{2} \pm\frac{5}{2}$
    $x_1=\color{blue}{2} \quad x_2=\color{green}{-3}$

    => Definitionslücken bei $x_1=\color{blue}{2}$ und $x_2=\color{green}{-3}$

  2. Nullstellen des Nenners in Zähler einsetzen

    $3x-6$

    $3\cdot\color{blue}{2}-6=0$
    => $x_1=2$ ist eine Nullstelle des Zählers

    $3\cdot\color{green}{-3}-6=-15$
    => $x_2=-3$ ist keine Nullstelle des Zählers

  3. Bedingung überprüfen

    Die Nullstelle mit $x_2=-3$ des Nenners ist keine Nullstelle des Zählers. Die Bedingung ist erfüllt:
    Bei $x_2=-3$ handelt es sich um eine Polstelle der Funktion.

    Die Nullstelle mit $x_1=2$ des Nenners ist auch eine Nullstelle des Zählers. Die Bedingung ist nicht erfüllt:
    Die Stelle kann Polstelle oder hebbare Definitionslücke sein.

  4. Kürzen: Prüfen, ob Polstelle oder hebbare Definitionslücke

    Faktorisieren
    $f(x)=\frac{3x-6}{x^2+x-6}$ $=\frac{3(x-2)}{(x+3)(x-2)}$
    Kürzen
    $f(x)=\frac{3\color{red}{(x-2)}}{(x+3)\color{red}{(x-2)}}$ $=\frac{3}{x+3}$
    => Bei $x_1=2$ handelt es sich um eine hebbare Definitionslücke, denn sie kann durch Kürzen behoben (eliminiert) werden