Mathe ↠ Gebrochenrationale Funktionen ↠ Definitionsbereich und Definitionslücken

Definitionsbereich und Definitionslücken

Der Definitionsbereich gibt an, für welche Zahlen eine Funktion definiert ist. Bei einer gebrochenrationalen Funktion ist das die Menge der reellen Zahlen ohne die, bei denen das Nennerpolynom den Wert null annimmt.

!

Merke

Da durch Null nicht dividiert werden darf, sind die Zahlen, an denen das Nennerpolynom den Wert null annimmt, nicht definiert. Diese Zahlen nennt man Definitionslücke.

Zusammengefasst: Die Nullstellen des Nenners sind Definitionslücken. Alle Zahlen außer der Definitionslücken bilden den Definitionsbereich.

i

Tipp

Eine gebrochenrationale Funktion kann eine, mehrere oder keine Definitionslücken haben.

Eine Definitionslücke kann entweder eine Polstelle oder eine hebbare Definitionslücke sein.

Beispiel

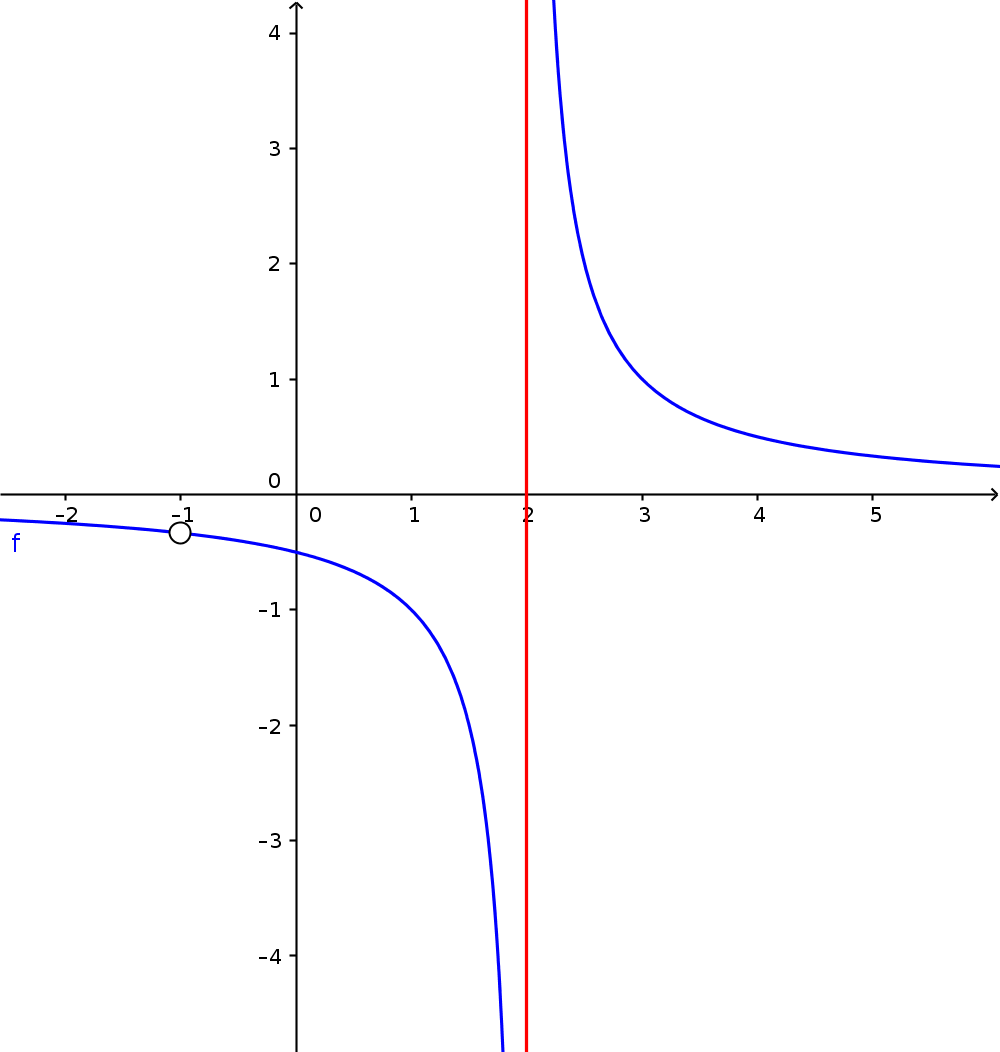
Im Beispiel sieht man, dass der Graph zwei Definitionslücken aufweist:

  1. Die Definitionslücke bei $x=2$ nennt man eine Polstelle. Die Funktionswerte verlaufen an dieser Stelle gegen unendlich.
  2. Die zweite Definitionslücke am Punkt $x=-1$ ist eine hebbare Definitionslücke.

Bestimmen von Definitionslücken / Definitionsbereich

Zuerst wird/werden die Definitionslücke(n) bestimmt, indem man herausfindet für welche Einsetzungen der Nenner den Wert Null annimmt. Dann schließt man diese vom Definitionsbereich aus.

i

Vorgehensweise

  1. Nenner gleich Null setzen
  2. Gleichung lösen
  3. Definitionsbereich angeben

Beispiel

Aufgabe: Gib den Definitionsbereich der Funktion an.

$f(x)=\frac{x+1}{x^2-x-2}$

  1. Nenner gleich Null setzen

    $x^2-x-2=0$

  2. Gleichung lösen

    In diesem Beispiel haben wir nun eine quadratische Gleichung, die wir beispielsweise mit der PQ-Formel lösen können.
    $x_{1,2} = -\frac{p}{2} \pm\sqrt{(\frac{p}{2})^2-q}$
    $x_{1,2} = \frac{1}{2} \pm\sqrt{(\frac{1}{2})^2+2}$
    $x_{1,2} = \frac{1}{2} \pm\sqrt{\frac{9}{4}}$
    $x_{1,2} = \frac{1}{2} \pm\frac{3}{2}$
    $x_1=2 \quad x_2=-1$

    => Definitionslücken bei $x_1=2$ und $x_2=-1$ (siehe Beispielbild oben)

  3. Definitionsbereich angeben

    Der Definitionsbereich sind alle reellen Zahlen außer Definitionslücken
    $D=\mathbb{R}\backslash\{2; -1\}$