Asymptoten

Eine Geraden, an die sich die Funktion annähert aber niemals erreicht, nennt man eine Asymptote.

Senkrechte Asymptoten

Polstellen sind daher senkrechte Asymptoten.

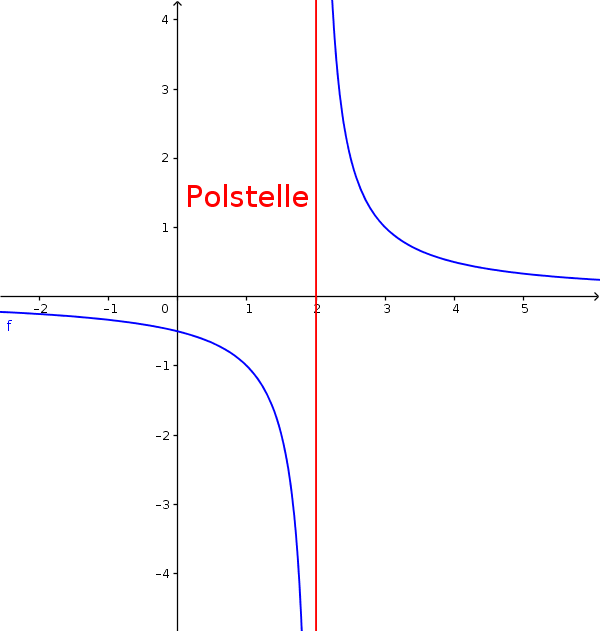
(Berechnung siehe Polstellen)

Schiefe Asymptoten

Eine weitere Art sind die schiefen Asymptoten.

Deren Funktionsgleichungen können mit Polynomdivision ermittelt werden.

Nur unecht gebrochenrationalen Funktionen (Zählergrad > Nennergrad) haben schiefe Asymptoten.

i

Vorgehensweise

  1. Bedingung überprüfen
  2. Polynomdivision
  3. Asymptotengleichung ablesen

Beispiel

$f(x)=\frac{x^2-3x-4}{x+2}$

  1. Bedingung überprüfen

    Ist der Zählergrad größer als der Nennergrad?

    Der Zählergrad ist 2 (da $x^\color{red}{2}$). Der Nennergrad ist 1 (da nur $x^\color{red}{1}$). Die Bedingung ist erfüllt.

  2. Polynomdivision

  3. Asymptotengleichung ablesen

    Die Gleichung der Asymptoten kann nun leicht aus dem Ergebnis abgelesen werden. Der ganzrationale Teil ("ohne Bruch") wird nun gleich y gesetzt.

    $y=\color{red}{x-5}$

    Damit haben wir unsere Asymptotengleichung.