Verhalten im Unendlichen
Der Grenzwert sagt aus, wie sich eine Funktion bei sehr großen ($+\infty$) oder sehr kleinen Zahlen ($-\infty$) verhalten wird.
Tipp
Zur Bestimmung des Grenzwertes, fragt man sich also: „Welche Zahl würde bei unendlich erreicht werden?“
Am einfachsten ist es mit einer Wertetabelle möglichst große oder kleine Zahlen in die Funktion einzusetzen.
Beispiel
$f(x)=\frac{x+1}{x^2-x-2}$
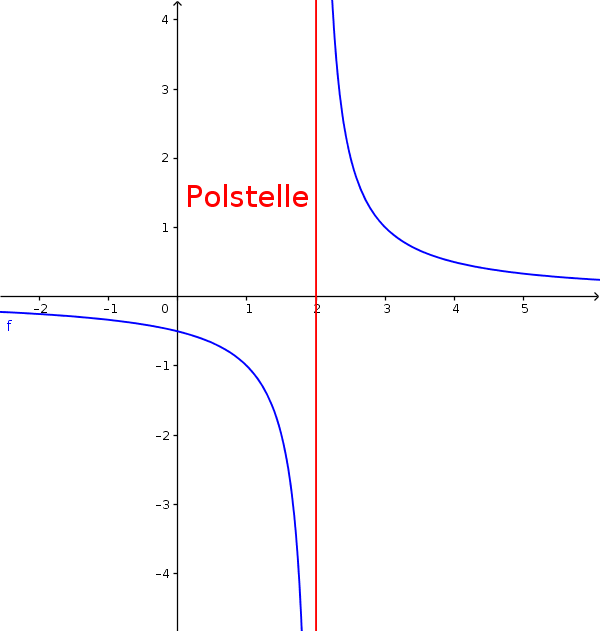
Am Graphen kann man bereits erkennen, dass die Funktion sowohl nach $+\infty$ (nach rechts) als auch nach $-\infty$ (nach links) den Grenzwert null hat. Denn je höher (kleiner) x ist, desto näher kommt die Funktion der 0.
Die Wertetabelle für $+\infty$ könnte so aussehen:
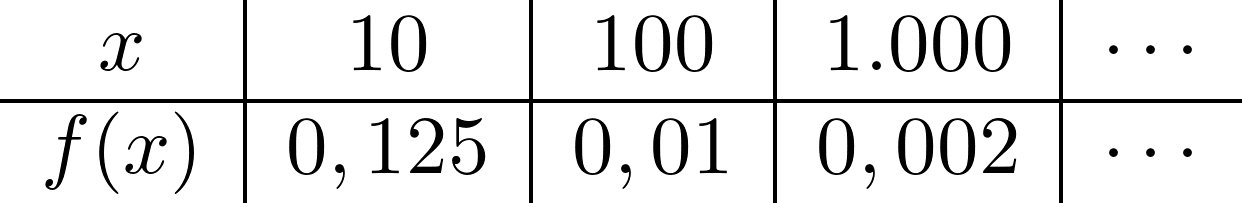
Die y-Werte werden immer kleiner, nähern sich der null, aber erreichen sie nie. Wir können also sagen, der Grenzwert für $+\infty$ ist 0.
Statt Grenzwert sagt man auch häufig Limes. In der Mathematik schreibt man daher $\lim$ und darunter welche „Richtung“ man betrachtet hat ($+\infty$ oder $-\infty$). Hinter das Limes kommt die Funktion und schließlich ein Gleichzeichen sowie der ermittelte Grenzwert.
$\lim\limits_{x\to+\infty} \frac{x+1}{x^2-x-2}=0$
Merke
$\lim\limits_{x\to+\infty} f(x)=\,?$
gelesen: limes von f von x für x gegen unendlich ist ...
