Polynomdivision
Kubische Gleichungen sind Gleichungen 3. Grades und besitzen die Form:
Um kubische Gleichungen und Gleichungen höheren Grades zu lösen, benötigt man die Polynomdivision.
Zuerst wird eine Nullstelle durch Probieren erraten und danach kann man mit Polynomdivision die Gleichung zu einer quadratischen Gleichung transformieren.
Vorgehensweise
- Nullstelle raten
- Polynomdivision: Gleichung durch $(x-x_N)$ teilen
- Quadratische Gleichung lösen
Tipp
Beispiel
Kubische Gleichung lösen: $x^3-19x-30=0$
-
Nullstelle raten
Die erste Nullstelle muss durch Probieren gefunden werden.
Dazu verschiedene Werte für $x$ einsetzen bis 0 rauskommt.
$x^3-19x-30=0$
$x=1$:
$1^3-19\cdot1-30=-48$ $\neq0$ =>keine Nullstelle
$x=-1$:
$(-1)^3-19\cdot(-1)-30=-12$ $\neq0$ =>keine Nullstelle
$x=-2$:
$(-2)^3-19\cdot(-2)-30=-0$ =>Nullstelle bei $x_{1}=-2$ -
Polynomdivision
Die Funktion wird durch $(x-x_1)$ geteilt. Dazu Polynomdivision nutzen.
$(x^3-19x-30):(x+2)$Zuerst rechnet man $x^3:x$ und schreibt das Ergebnis auf.

Jetzt wird $x^2$ mit $(x+2)$ multipliziert. Das Ergebnis kommt in die zweite Zeile und erhält ein Minus.

Beide Zeilen werden nun zusammengerechnet, wobei der Rest darunter geschrieben wird.
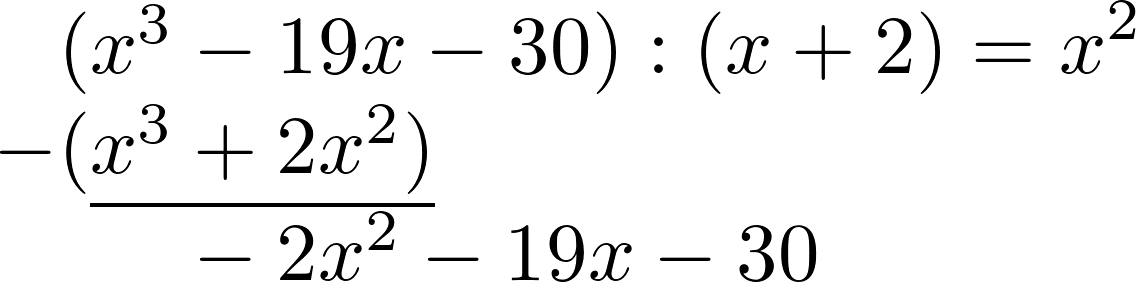
Ähnlich wie vorher rechnet man nun $-2x^2:x$. Das Ergebnis schreibt man rechts hin und multipliziert es wieder mit $(x+2)$ um es in die Zeile darunter zu schreiben.
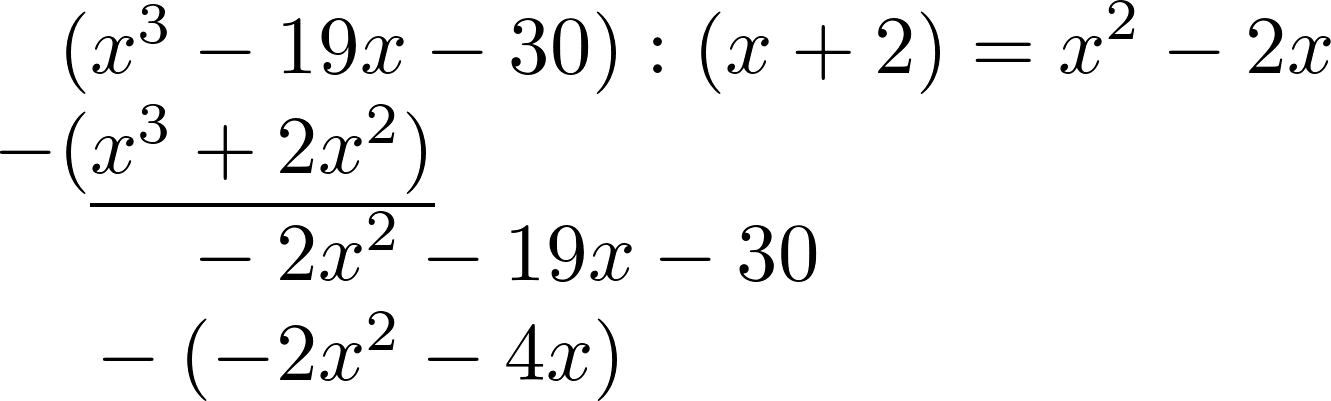
Die beiden Zeilen werden erneut abgezogen.
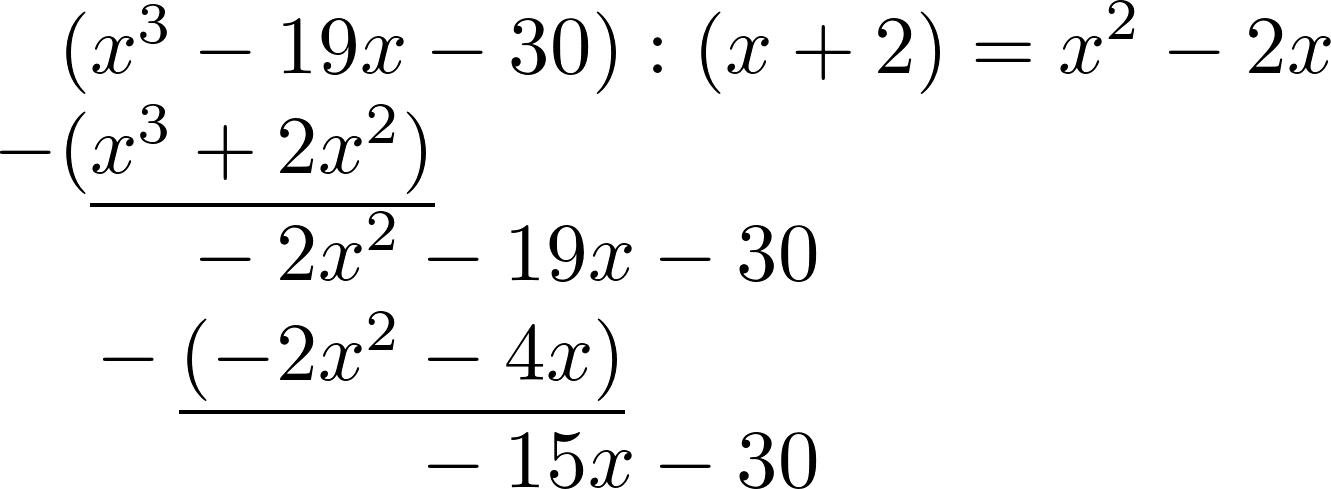
Schließlich wird noch $-15x:x$ gerechnet, zurück multipliziert und abgezogen. Der Rest ist 0 und die Polynomdivision ist fertig.
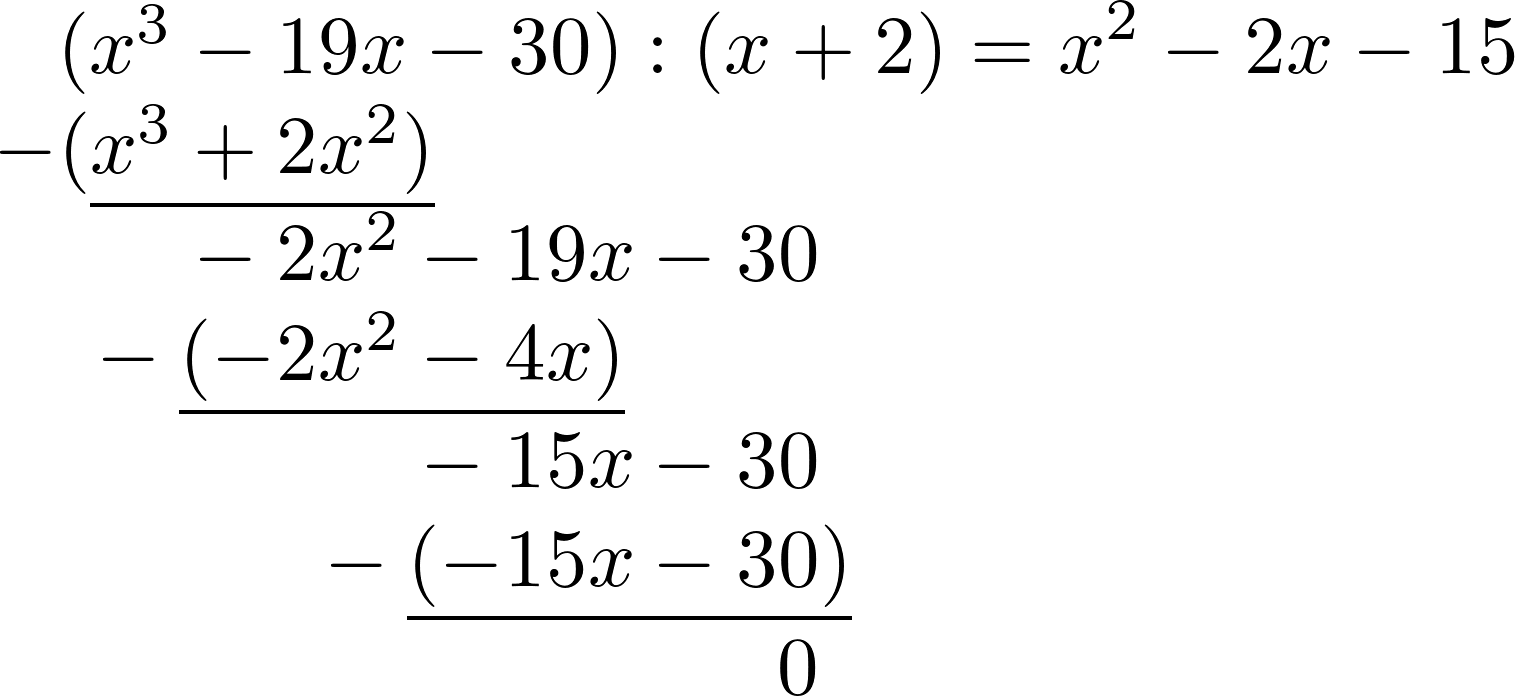
-
Quadratische Gleichung lösen
Die neue quadratische Gleichung kann man nun lösen z. B. PQ-Formel.
$x^2-2x-15=0$
$x_{2,3} = \frac{p}{2} \pm\sqrt{(\frac{p}{2})^2-q}$
$x_{2,3} = 1 \pm\sqrt{1^2+15}$
$x_{2,3} = 1 \pm\sqrt{16}$
$x_{2,3} = 1 \pm4$
$x_2=5$ und $x_3=-3$
Die Lösungen der Ausgangsgleichung sind $x_1=-2$, $x_2=5$ und $x_3=-3$

